题目内容
2.若O为△ABC内一点,且2$\overrightarrow{OA}$$+7\overrightarrow{OB}$$+6\overrightarrow{OC}$=$\overrightarrow{0}$,三角形ABC的面积是三角形OAB面积的λ倍,则λ=( )| A. | $\frac{5}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{15}{7}$ | D. | 5 |
分析 如图所示,作$\overrightarrow{OD}=2\overrightarrow{OA}$,$\overrightarrow{OE}=7\overrightarrow{OB}$,$\overrightarrow{OF}=6\overrightarrow{OC}$.由于2$\overrightarrow{OA}$$+7\overrightarrow{OB}$$+6\overrightarrow{OC}$=$\overrightarrow{0}$,可得:点O是△DEF的重心.可得$\frac{S△OAB}{{S}_{△OED}}$=$\frac{1}{14}$,S△OAB=$\frac{1}{3}×\frac{1}{14}$×S△DEF=$\frac{1}{42}$S△DEF,同理可得:S△OBC=$\frac{1}{126}$S△DEF,S△OAC=$\frac{1}{36}$S△DEF.即可得出.
解答 解:如图所示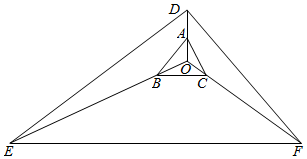
作$\overrightarrow{OD}=2\overrightarrow{OA}$,$\overrightarrow{OE}=7\overrightarrow{OB}$,$\overrightarrow{OF}=6\overrightarrow{OC}$.
∵2$\overrightarrow{OA}$$+7\overrightarrow{OB}$$+6\overrightarrow{OC}$=$\overrightarrow{0}$,
∴点O是△DEF的重心.
可得$\frac{S△OAB}{{S}_{△OED}}$=$\frac{OA×OB}{2OA×70B}$=$\frac{1}{14}$,
∴S△OAB=$\frac{1}{3}×\frac{1}{14}$×S△DEF=$\frac{1}{42}$S△DEF,
同理可得:S△OBC=$\frac{1}{126}$S△DEF,S△OAC=$\frac{1}{36}$S△DEF.
∴S△OAB=S△ABC$\frac{1}{14}$÷$(\frac{1}{42}+\frac{1}{126}+\frac{1}{36})$=$\frac{2}{5}$S△ABC,
∴$λ=\frac{5}{2}$.
故选:A.
点评 本题考查了向量的三角形法则、共面向量基本定理、三角形重心性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅱ)已知每辆该型号汽车的收购价格为w=0.05x2-1.75x+17.2万元,根据(Ⅰ)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润z最大?
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
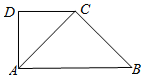 已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.