题目内容
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{x-y≥1}\\{y≥-2}\end{array}\right.$,则$z={log_{13}}\sqrt{{x^2}+{y^2}}$的最大值为$\frac{1}{2}$.分析 y=log13x在其定义域上是增函数,故转化为求$\sqrt{{x}^{2}+{y}^{2}}$的最大值,利用线性规划求最值即可.
解答 解:由题意作平面区域如下,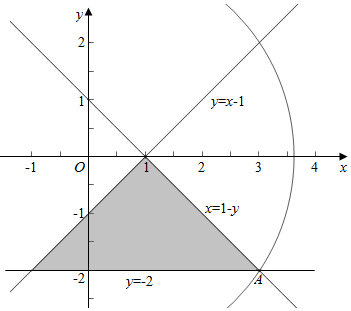
结合图象可知,
当过点A(3,-2)时,$\sqrt{{x}^{2}+{y}^{2}}$取得最大值$\sqrt{9+4}$=$\sqrt{13}$,
此时$z={log_{13}}\sqrt{{x^2}+{y^2}}$有最大值log13$\sqrt{13}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了学生的作图能力及线性规划的应用,同时考查了数形结合的思想应用及对数函数的单调性的应用.

练习册系列答案
相关题目
18.已知f(x)=2sin(2x+$\frac{π}{6}$),若将它的图象向右平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则函数g(x)的图象的一个对称中心为( )
| A. | (0,0) | B. | ($\frac{π}{6}$,0) | C. | ($\frac{π}{12}$,0) | D. | ($\frac{π}{4}$,0) |
19.若p:a,b∈R+;q:a2+b2≥2ab,则( )
| A. | p是q充要条件 | |
| B. | p是q的充分条件,但不是q的必要条件 | |
| C. | p是q的必要条件,但不是q的充分条件 | |
| D. | p既不是q的充分条件,也不是q的必要条件 |
13.已知指数函数y=f(x)的图象过点P(3,27),则在(0,10]内任取一个实数x,使得f(x)>81的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
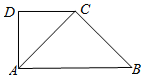 已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.
已知梯形ABCD如图所示,连接AC,AD:DC:AC:BC:AB=1:1:$\sqrt{2}$:$\sqrt{2}$:2,现沿AC将梯形ABCD折叠成三棱锥D-ABC,则当三棱锥D-ABC的体积最大时,二面角D-AB-C的正切值为$\sqrt{2}$.