题目内容
5．若x2+2xy-y2=7（x，y∈R）．求x2+y2的最小值．分析 设x2+y2=r2，则x=rcosa，y=rsina，从而化简可得$\sqrt{2}$r2sin（2a+$\frac{π}{4}$）=7，从而求最小值．
解答 解：设x2+y2=r2，则x=rcosa，y=rsina，
则x2+2xy-y2=7可化为
r2cos2a+2r2sinacosa-r2sin2a=7，
即r2（cos2a+sin2a）=7，
即$\sqrt{2}$r2sin（2a+$\frac{π}{4}$）=7，
故当sin（2a+$\frac{π}{4}$）=1时，r2有最小值为$\frac{7\sqrt{2}}{2}$，
故x2+y2的最小值为$\frac{7\sqrt{2}}{2}$．
点评 本题考查了参数法的应用及三角恒等变换的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．已知指数函数y=f（x）的图象过点P（3，27），则在（0，10]内任取一个实数x，使得f（x）＞81的概率为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{7}{10}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
10．二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：
（Ⅰ）试求y关于x的回归直线方程；（参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}^{2}}_{i}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
（Ⅱ）已知每辆该型号汽车的收购价格为w=0.05x2-1.75x+17.2万元，根据（Ⅰ）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润z最大？
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
（Ⅱ）已知每辆该型号汽车的收购价格为w=0.05x2-1.75x+17.2万元，根据（Ⅰ）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润z最大？
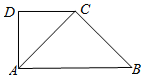已知梯形ABCD如图所示，连接AC，AD：DC：AC：BC：AB=1：1：$\sqrt{2}$：$\sqrt{2}$：2，现沿AC将梯形ABCD折叠成三棱锥D-ABC，则当三棱锥D-ABC的体积最大时，二面角D-AB-C的正切值为$\sqrt{2}$．