题目内容
已知f(x)=asinx+bx+c(a,b,c∈R),若f(0)=-2,f(
)=1,则f(-
)= .
| π |
| 2 |
| π |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由f(0)=-2求得c的值,再由f(
)=1求得asin
+b
=3.则f(-
)可求.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:
解:∵f(x)=asinx+bx+c,且f(0)=-2,
∴c=-2.
又f(
)=1,
∴asin
+b•
-2=1,即asin
+b
=3.
∴f(-
)=asin(-
)-b•
-2=-(asin
+b•
)-2=-3-2=-5.
故答案为:-5.
∴c=-2.
又f(
| π |
| 2 |
∴asin
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴f(-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:-5.
点评:本题考查了函数奇偶性的性质,关键在于转化,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若抛物线的顶点为坐标原点,焦点为(0,1),则此抛物线的方程是( )
| A、y2=2x |
| B、y2=4x |
| C、x2=2y |
| D、x2=4y |
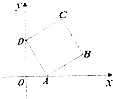 如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则
如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则