题目内容
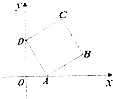 如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则
如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则| OB |
| OC |
| ||
| 2 |
考点:几何概型
专题:综合题,概率与统计
分析:设∠OAD=θ,0<θ<
.可得xB=2cosθ+2sinθ,yB=2cosθ,xC=2sinθ,yC=2sinθ+2cosθ.再利用数量积运算、同角三角函数基本关系式、倍角公式、正弦函数的单调性有界性得出4<
•
≤8,即可求出概率.
| π |
| 2 |
| OB |
| OC |
解答:
解:设∠OAD=θ,0<θ<
.
则xB=cosθ+sinθ,yB=cosθ,xC=sinθ,yC=sinθ+cosθ.
∴B(cosθ+sinθ,cosθ),C(sinθ,sinθ+cosθ),
∴
•
=(cosθ+sinθ,cosθ)•(sinθ,sinθ+cosθ)
=(cosθ+sinθ)×sinθ+cosθ(sinθ+cosθ)
=sinθcosθ+sin2θ+sinθcosθ+cos2θ
=sin2θ+1.
∵0<θ<
,
∴0<2θ<π,
∴0<sin2θ≤1.
∴1<sin2θ+1≤2.
∴1<
•
≤2,
∵
•
≥1+
,
∴
•
≥1+
的概率为
-1.
故答案为:
-1.
| π |
| 2 |
则xB=cosθ+sinθ,yB=cosθ,xC=sinθ,yC=sinθ+cosθ.
∴B(cosθ+sinθ,cosθ),C(sinθ,sinθ+cosθ),
∴
| OB |
| OC |
=(cosθ+sinθ)×sinθ+cosθ(sinθ+cosθ)
=sinθcosθ+sin2θ+sinθcosθ+cos2θ
=sin2θ+1.
∵0<θ<
| π |
| 2 |
∴0<2θ<π,
∴0<sin2θ≤1.
∴1<sin2θ+1≤2.
∴1<
| OB |
| OC |
∵
| OB |
| OC |
| ||
| 2 |
∴
| OB |
| OC |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题综合考查了数量积运算、同角三角函数基本关系式、倍角公式、正弦函数的单调性有界性,考查了计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

