题目内容
9.在△ABC中,角A,B,C的对边分别为a,b,c,bcos2$\frac{A}{2}$+acos2$\frac{B}{2}$=$\frac{3}{2}$c.(1)求证:a,c,b成等差数列;
(2)若C=$\frac{π}{3}$,△ABC的面积为2$\sqrt{3}$,求c.
分析 (1)利用正弦定理、二倍角公式、诱导公式,证得sinB+sinA=2sinC,可得a,c,b成等差数列.
(2)根据C=$\frac{π}{3}$,△ABC的面积为2$\sqrt{3}$,求得ab的值,再利用余弦定理求得c的值.
解答 解:(Ⅰ)证明:△ABC中,∵bcos2$\frac{A}{2}$+acos2$\frac{B}{2}$=$\frac{3c}{2}$c,由正弦定理得:
sinBcos2$\frac{A}{2}$+sinAcos2$\frac{B}{2}$=$\frac{3}{2}$sinC,
即sinB•$\frac{1+cosA}{2}$+sinA•$\frac{1+cosB}{2}$=$\frac{3}{2}$sinC,
∴sinB+sinA+sinBcosA+cosBsinA=3sinC,
∴sinB+sinA+sin(A+B)=3sinC,
∴sinB+sinA+sinC=3sinC,∴sinB+sinA=2sinC∴a+b=2c,
∴a,c,b成等差数列.
(Ⅱ)∵C=$\frac{π}{3}$,△ABC的面积为S=$\frac{1}{2}$ab•sinC=2$\sqrt{3}$,∴ab=8,
又c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab=4c2-24,
∴c2=8,可得c=2$\sqrt{2}$.
点评 本题主要考查正弦定理、余弦定理的应用,诱导公式,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
17.已知命题p:“?x0∈R,x03>x0”,则命题¬p为( )
| A. | ?x∈R,x3>x | B. | ?x∈R,x3<x | C. | ?x∈R,x3≤x | D. | ?x0∈R,x03≤x0 |
1.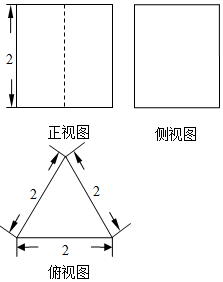 如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
 如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )| A. | $\frac{49}{9}π$ | B. | $\frac{{28\sqrt{21}}}{27}π$ | C. | $\frac{28}{3}π$ | D. | $\frac{{28\sqrt{7}}}{9}π$ |
18.函数$y=tan(2x-\frac{π}{3})$的最小正周期是( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
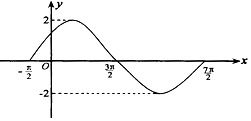 已知f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)在一个周期内图象如图所示.
已知f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)在一个周期内图象如图所示.