题目内容
已知数列{an}满足a1=1,an+1-an=2n(n∈N),Sn是数列{an}的前n项和,则S2012= .
考点:数列的求和
专题:等差数列与等比数列
分析:由于an+1-an=2n(n∈N),利用“累加求和”可得an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n2-n+1,即可得出Sn=(12+22+…+n2)-(1+2+…+n)+n=
-
+n.
=n2-n+1,即可得出Sn=(12+22+…+n2)-(1+2+…+n)+n=
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
解答:
解:∵an+1-an=2n(n∈N),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2+1
=
+1
=n2-n+1,
∴Sn=(12+22+…+n2)-(1+2+…+n)+n
=
-
+n.
∴S2012=27169779084.
故答案为:27169779084.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2+1
=
| 2×(n-1)(1+n-1) |
| 2 |
=n2-n+1,
∴Sn=(12+22+…+n2)-(1+2+…+n)+n
=
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
∴S2012=27169779084.
故答案为:27169779084.
点评:本题考查了“累加求和”、等差数列的前n项和公式及其公式(12+22+…+n2)=
-
+n,考查了推理能力与计算能力,属于中档题.
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |

练习册系列答案
相关题目
在下列关于点P,直线l、m与平面α、β的命题中,正确的是( )
| A、若m⊥α,l⊥m,则l∥α |
| B、若α⊥β,α∩β=m,P∈α,P∈l,且l⊥m,则l⊥β |
| C、若l,m是异面直线,m?α,m∥β,l?β,l∥α,则α∥β |
| D、若α⊥β,且l⊥β,m⊥l,则m⊥α |
设x,y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|

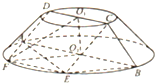 如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.
如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.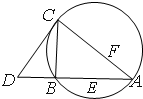 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.