题目内容
若α∈(-
,
],则cosα的范围是( )
| π |
| 6 |
| π |
| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、[
| ||||||
D、[
|
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:由余弦函数的单调性可知cosα在(-
,0]上是单调递增的,在[0,
]上是单调递减的,即可求出cosα的范围.
| π |
| 6 |
| π |
| 3 |
解答:
解:∵cosα在(-
,0]上是单调递增的,在[0,
]上是单调递减的,故cosαmax=cos0=1;
又cos(-
)=
>cos
=
,故有cosαmin=cos
=
.
故选:C.
| π |
| 6 |
| π |
| 3 |
又cos(-
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
故选:C.
点评:本题主要考察了余弦函数的图象和性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x,y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
数列3,7,13,21,31,…的一个通项公式是( )
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n(n2-1) |
设f(x)=2x-3,g(x+2)=f(x),则g(x)=( )
| A、2x+1 | B、2x+3 |
| C、2x-7 | D、2x-3 |
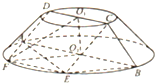 如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.
如图所示,圆台上、下底面半径分别为4,8,母线与底面所成角为45°,平面ABCD为圆台的轴截面,E为下底面圆弧上一点,且∠ABE=60°,过CDE的平面交⊙O2于点F.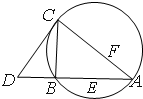 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.