题目内容
设F1，F2是双曲线C：
-
=1（a＞0，b＞0）的两个焦点，P是C上一点，若|PF1|+|PF2|=6a，|PF1|＞|PF2|，∠PF1F2=30°，则C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、2
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义得|PF1|-|PF2|=2a，结合题中等式算出|PF1|=4a且|PF2|=2a，进而利用余弦定理算出|F1F2|=2
a，再由离心率公式可算出该双曲线的离心率．
| 3 |
解答：
解：∵|PF1|+|PF2|=6a，|PF1|-|PF2|=2a，
∴|PF1|=4a且|PF2|=2a，
又∵∠PF1F2=30°，
∴根据余弦定理，得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos30°=12a2
因此，|F1F2|=2
a，可得双曲线的离心率e=
=
=
．
故选：A
∴|PF1|=4a且|PF2|=2a，
又∵∠PF1F2=30°，
∴根据余弦定理，得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos30°=12a2
因此，|F1F2|=2
| 3 |
| 2c |
| 2a |
2
| ||
| 2a |
| 3 |
故选：A
点评：本题给出双曲线满足的条件，求它的离心率．考查了双曲线的定义与标准方程、余弦定理等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
下列命题：
（1）若f（x）是增函数，则
是减函数；
（2）若f（x）是减函数，则[f（x）]2是减函数；
（3）若f（x）是增函数，g（x）是减函数，g[f（x）]有意义，则g[f（x）]为减函数，
其中正确的个数有（ ）
（1）若f（x）是增函数，则
| 1 |
| f(x) |
（2）若f（x）是减函数，则[f（x）]2是减函数；
（3）若f（x）是增函数，g（x）是减函数，g[f（x）]有意义，则g[f（x）]为减函数，
其中正确的个数有（ ）
| A、1 | B、2 | C、3 | D、0 |
已知曲线y=2x3上一点A（1，2），则A处切线的斜率是（ ）
| A、2 | B、3 | C、4 | D、6 |
已知集合A={x|-2≤x≤3}，B={x|-1≤x≤4}，那么集合A∩B等于（ ）
| A、{x|-2≤x≤4} |
| B、{x|3≤x≤4} |
| C、{x|-2≤x≤-1} |
| D、{x|-1≤x≤3} |
抛物线y2=20x的焦点坐标为（ ）
| A、（10，0） |
| B、（5，0） |
| C、（0，10） |
| D、（0，5） |
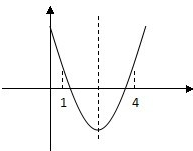已知关于x不等式x2-2ax+a+2≤0（a∈R）的解集为M．
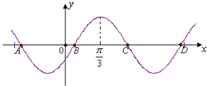已知函数f（x）=sin（ωx+φ）（ω＞0）的部分图象如图所示，点B（