题目内容
已知数列{an}的前n项和为Sn,且满足a2=6,3Sn=(n+1)an+n(n+1).
(1)求a1,a3;
(2)求数列{an}的通项公式.
(1)求a1,a3;
(2)求数列{an}的通项公式.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)分别令n=1,n=3,建立方程即可求a1,a3;
(2)由数列的递推关系,构建方程组,即可求数列{an}的通项公式;
(2)由数列的递推关系,构建方程组,即可求数列{an}的通项公式;
解答:
解 (1)令n=1得3a1=2a1+2,解得a1=2;
令n=3得3(8+a3)=4a2+12,解得a3=12.
(2)由已知3Sn=(n+1)an+n(n+1),①
3Sn+1=(n+2)an+1+(n+1)(n+2),②
②-①得3an+1=(n+2)an+1-(n+1)an+2(n+1),
即(n-1)an+1-(n+1)an+2(n+1)=0,③
所以nan+2-(n+2)an+1+2(n+2)=0,④
④-③得nan+2-(2n+1)an+1+(n+1)an+2=0,
即n(an+2-an+1)-(n+1)(an+1-an)+2=0,⑤
从而(n+1)(an+3-an+2)-(n+2)(an+2-an+1)+2=0,⑥
⑥-⑤得(n+1)(an+3-an+2)-2(n+1)(an+2-an+1)+(n+1)(an+1-an)=0,
即(an+3-an+2)-2(an+2-an+1)+(an+1-an)=0,
即(an+3-an+2)-(an+2-an+1)=(an+2-an+1)-(an+1-an),⑦
所以数列{an+1-an}是等差数列,首项为a2-a1=4,公差为(a3-a2)-(a2-a1)=2,
所以an+1-an=4+2(n-1)=2n+2,
即an-an-1=2n,an-1-an-2=2(n-1),…a3-a2=6,a2-a1=4,a1=2,
相加得an=2+4+6+…+2(n-1)+2n=n(n+1).
令n=3得3(8+a3)=4a2+12,解得a3=12.
(2)由已知3Sn=(n+1)an+n(n+1),①
3Sn+1=(n+2)an+1+(n+1)(n+2),②
②-①得3an+1=(n+2)an+1-(n+1)an+2(n+1),
即(n-1)an+1-(n+1)an+2(n+1)=0,③
所以nan+2-(n+2)an+1+2(n+2)=0,④
④-③得nan+2-(2n+1)an+1+(n+1)an+2=0,
即n(an+2-an+1)-(n+1)(an+1-an)+2=0,⑤
从而(n+1)(an+3-an+2)-(n+2)(an+2-an+1)+2=0,⑥
⑥-⑤得(n+1)(an+3-an+2)-2(n+1)(an+2-an+1)+(n+1)(an+1-an)=0,
即(an+3-an+2)-2(an+2-an+1)+(an+1-an)=0,
即(an+3-an+2)-(an+2-an+1)=(an+2-an+1)-(an+1-an),⑦
所以数列{an+1-an}是等差数列,首项为a2-a1=4,公差为(a3-a2)-(a2-a1)=2,
所以an+1-an=4+2(n-1)=2n+2,
即an-an-1=2n,an-1-an-2=2(n-1),…a3-a2=6,a2-a1=4,a1=2,
相加得an=2+4+6+…+2(n-1)+2n=n(n+1).
点评:本题主要考查数列通项公式,运算量较大,综合性较强,考查学生的计算能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知函数f(x)=5x-3sinx,x∈(-2,2),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A、(1,
| ||
| B、(1,3) | ||
| C、(-∞,-2)∪(1,+∞) | ||
| D、(-2,1) |
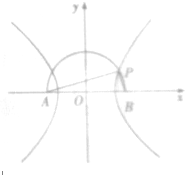 如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是
如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是