题目内容
已知函数f(x)=
,定义an=f(n),bn=log3(
an+1).
(1)求数列{bn}的通项公式;
(2)求满足方程
+
+…+
=
的正整数n的值.
| 2 |
| 3x |
| 1 |
| 2 |
(1)求数列{bn}的通项公式;
(2)求满足方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
考点:数列的求和,数列与函数的综合
专题:等差数列与等比数列
分析:(1)由an=f(n)=
,可得bn=-n-1.
(2)由(1)可得
=
=
-
.因此方程
+
+…+
=
,化为
-
=
,即可解出.
| 2 |
| 3n |
(2)由(1)可得
| 1 |
| bnbn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
| 1 |
| 2 |
| 1 |
| n+2 |
| 25 |
| 51 |
解答:
解:(1)∵an=f(n)=
,
∴bn=log3(
an+1)=log3(
×
)=-n-1.
(2)由(1)可得
=
=
-
.
∴方程
+
+…+
=
,化为(
-
)+(
-
)+(
-
)=
-
=
,
解得n=49.
| 2 |
| 3n |
∴bn=log3(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3n+1 |
(2)由(1)可得
| 1 |
| bnbn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| 25 |
| 51 |
解得n=49.
点评:本题考查了对数的运算性质、递推式的应用、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=1-sinx,x∈[0,2π]的图象与直线y=
交点的个数是( )
| 3 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
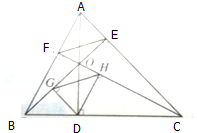 如图所示,已知AD,BE,CF是△ABC的三条高,DG⊥BE于点G,DH⊥CF于点H,求证:HG∥EF.
如图所示,已知AD,BE,CF是△ABC的三条高,DG⊥BE于点G,DH⊥CF于点H,求证:HG∥EF.