题目内容
二次函数f(x)=x2-2x
(1)写出f(x)单调区间
(2)写出f(x)的值域
(3)若f(x)=x2-2x,x∈[-2,2],求f(x)的最大,最小值.
(1)写出f(x)单调区间
(2)写出f(x)的值域
(3)若f(x)=x2-2x,x∈[-2,2],求f(x)的最大,最小值.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)对称轴x=1,根据二次函数性质求解,
(2)根据单调性求解x=1时,最小值为f(1)=1-2=-1,即可得出值域.
(3)判断出单调递减区间为[-2,1],单调递增区间[1,2],
ymin=f(1)=-1,ymax=f(-2)=8.
(2)根据单调性求解x=1时,最小值为f(1)=1-2=-1,即可得出值域.
(3)判断出单调递减区间为[-2,1],单调递增区间[1,2],
ymin=f(1)=-1,ymax=f(-2)=8.
解答:
解:(1)∵二次函数f(x)=x2-2x,
∴对称轴x=1
即单调递减区间为(-∞,1],单调递增区间[1,+∞)
(2)∵x=1时,最小值为f(1)=1-2=-1,
∴f(x)的值域为:[-1,+∞)
(3)∵f(x)=x2-2x,x∈[-2,2],
∴对称轴x=1,
∵单调递减区间为[-2,1],单调递增区间[1,2],
∴ymin=f(1)=-1,ymax=f(-2)=8.
即ymin=-1,ymax=8
∴对称轴x=1
即单调递减区间为(-∞,1],单调递增区间[1,+∞)
(2)∵x=1时,最小值为f(1)=1-2=-1,
∴f(x)的值域为:[-1,+∞)
(3)∵f(x)=x2-2x,x∈[-2,2],
∴对称轴x=1,
∵单调递减区间为[-2,1],单调递增区间[1,2],
∴ymin=f(1)=-1,ymax=f(-2)=8.
即ymin=-1,ymax=8
点评:本题考查了二次函数的基本性质,求解问题,难度不大,属于容易题,关键是根据对称轴,确定单调区间,最值问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正四面体ABCD中,M,N分别是棱BC、AD的中点,则异面直线AM,CN所成角的余弦值为( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
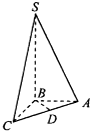 如图,在四面体S-ABC中,AB,BC,BS两两垂直,且AB=BC=2,BS=4,点D为AC的中点.若异面直线AS与BD所成角为θ,则cosθ的值为( )
如图,在四面体S-ABC中,AB,BC,BS两两垂直,且AB=BC=2,BS=4,点D为AC的中点.若异面直线AS与BD所成角为θ,则cosθ的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|