题目内容
20．已知函数f（x）=（x+a）（x-b），若a，b∈{-2，-1，0，1，2}，则f（x）为偶函数的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
分析 由已知f（x）为偶函数时，a=b，a，b∈{-2，-1，0，1，2}，先求出基本事件总数，再求出满足a=b的情况有几种，由此能求出f（x）为偶函数的概率．
解答 解：∵函数f（x）=（x+a）（x-b）=x2+（a-b）x-ab，
∴f（x）为偶函数时，a=b，
∵a，b∈{-2，-1，0，1，2}，
∴基本事件总数n=5×5=25，其中满足a=b的情况有：m=5种，
∴f（x）为偶函数的概率为p=$\frac{m}{n}=\frac{5}{25}=\frac{1}{5}$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
步步高达标卷系列答案
相关题目
8．已知函数y=x（x-2）的定义域为[a，b]，值域为[-1，3]，则点（a，b）对应图中的（ ）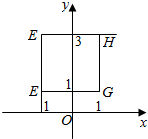
| A． | 点H（1，3）和点F（-1，1） | B． | 线段EF和线段GH | C． | 线段EH和线段FG | D． | 线段EF和线段EH |
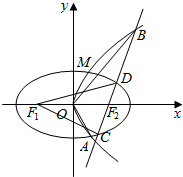如图，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）和抛物线C2：y2=2px（p＞0）都经过点M（$\frac{2}{3}$，$\frac{2\sqrt{6}}{3}$），且椭圆C1的右焦点和抛物线C2的焦点F2相同．