题目内容
10.已知过球面上三点A,B,C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=3cm,则球的体积是$\frac{32π}{3}$.分析 设出球的半径,解出△ABC的中心到顶点的距离,然后求出球的半径,则球的体积可求.
解答  解:设球的半径为2r,如图O为球心,E为BC的中点,D是三角形ABC的中心,
解:设球的半径为2r,如图O为球心,E为BC的中点,D是三角形ABC的中心,
那么AO2=OD2+AD2=OD2+$(\frac{2}{3}AE)^{2}$,
4r2=r2+[32-$(\frac{3}{2})^{2}$]×$(\frac{2}{3})^{2}$,
解得:r=1,
∴球的半径是2.
∴球的体积为:$\frac{32π}{3}$.
故答案为:$\frac{32π}{3}$.
点评 本题考查球的半径以及球的体积的求法,考查空间想象能力,是中档题.

练习册系列答案
相关题目
20.与610°角终边相同的角的集合( )
| A. | {a|a=k•360°+230°,k∈Z} | B. | {a|a=k•360°+250°,k∈Z} | ||
| C. | {a|a=k•360°+70°,k∈Z} | D. | {a|a=k•360°+270°,k∈Z} |
18.(题类B)设f(x)=sinx2,则f′(x)等于( )
| A. | sin2x | B. | cosx2 | C. | 2xsinx2 | D. | 2xcosx2 |
20.某种产品的广告费用支出x(千元)与销售额y(万元)之间有如下对应数据:
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}},\hat a=\bar y-\hat b\bar x$)
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
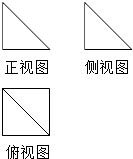 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.
一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.