题目内容
1.已知等差数列{an}的前n项和为Sn,且满足a32+a62=5,则S9的最大值是$\frac{9\sqrt{10}}{2}$.分析 利用等差数列性质及基本不等式求解.
解答 解:∵等差数列{an}的前n项和为Sn,且满足a32+a62=5,
∴${{a}_{3}}^{2}{{a}_{6}}^{2}≤\frac{25}{4}$,
∴${a}_{3}{a}_{6}≤\frac{5}{2}$,或$-\frac{5}{2}≤{a}_{3}{a}_{6}<0$,
由${a}_{3}{a}_{6}≤\frac{5}{2}$时,当且仅当a3=a6=$\frac{\sqrt{10}}{2}$时,取等号,
∴S9的最大值是$\frac{9\sqrt{10}}{2}$.
由$-\frac{5}{2}≤{a}_{3}{a}_{6}<0$,得S9的最大值小于$\frac{9\sqrt{10}}{2}$.
∴S9的最大值是$\frac{9\sqrt{10}}{2}$.
故答案为:$\frac{9\sqrt{10}}{2}$.
点评 本题考查数列的前9项和的求法,是基础题,解题时要认真审题,注意等差数列的性质及基本不等式性质的合理运用.

练习册系列答案
相关题目
6.在(1+x)3+(1+x)4+…+(1+x)2007的展开式中,x3的系数等于( )
| A. | $C_{2007}^4$ | B. | $C_{2007}^3$ | C. | $C_{2008}^4$ | D. | $C_{2008}^3$ |
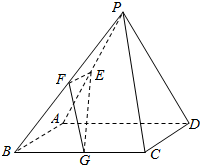 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.