题目内容
3．甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女，若从这6名教师中任选2名，选出的2名教师来自同一学校的概率为（ ）| A． | $\frac{5}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
分析 先求出基本事件总数n=${C}_{6}^{2}=15$，再求出选出的2名教师来自同一学校包含的基本事件个数m=${C}_{3}^{2}+{C}_{3}^{2}$=6，由此能求出选出的2名教师来自同一学校的概率．
解答 解：甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女，
从这6名教师中任选2名，
基本事件总数n=${C}_{6}^{2}=15$，
选出的2名教师来自同一学校包含的基本事件个数m=${C}_{3}^{2}+{C}_{3}^{2}$=6，
选出的2名教师来自同一学校的概率为p=$\frac{m}{n}$=$\frac{6}{15}=\frac{2}{5}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
13．
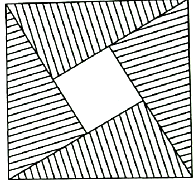如图所示，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形的概率为$\frac{1}{5}$，设直角三角形中较大的锐角为θ，则sinθ=（ ）
如图所示，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形的概率为$\frac{1}{5}$，设直角三角形中较大的锐角为θ，则sinθ=（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
1．设x＞0，y＞0，若不等式2log${\;}_{\frac{1}{2}}$[（a-1）x+ay]≤1+log${\;}_{\frac{1}{2}}$（xy）恒成立，则4a的最小值为（ ）
| A． | $\frac{\sqrt{6}+2}{4}$ | B． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C． | $\sqrt{6}$+2 | D． | $\sqrt{6}$+$\sqrt{2}$ |
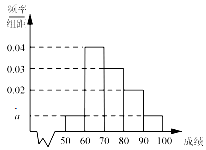某校100名学生期中考试物理成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．