题目内容
7.已知长方体ABCD-A1B1C1D1中,AB=BC,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{3}{5}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线BE与CD1所形成角的余弦值.
解答 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,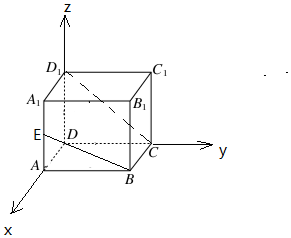
设AA1=2AB=2,
则B(1,1,0),E(1,0,1),C(0,1,0),D1(0,0,2),
$\overrightarrow{BE}$=(0,-1,1),$\overrightarrow{C{D}_{1}}$=(0,1,-2),
设异面直线BE与CD1所形成角为θ,
则cosθ=$\frac{|\overrightarrow{BE}•\overrightarrow{C{D}_{1}}|}{|\overrightarrow{BE}|•|\overrightarrow{C{D}_{1}}|}$=$\frac{3}{\sqrt{2}•\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
异面直线BE与CD1所形成角的余弦值为$\frac{3\sqrt{10}}{10}$.
故选:C.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.“x≥1”是“lgx≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.函数f(x)=$\frac{A}{sin(ωx+φ)}(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,则$f(\frac{3π}{2})$=( )
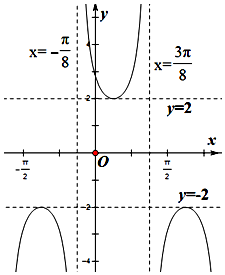

| A. | $2\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $-2\sqrt{2}$ |
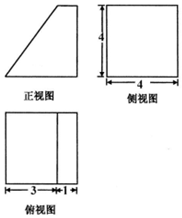 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是76cm2,体积是40cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是76cm2,体积是40cm3.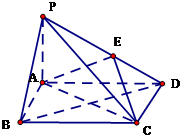 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.