题目内容
12.已知动点M到定点F(1,0)和定直线x=4的距离之比为$\frac{1}{2}$,设动点M的轨迹为曲线C.(1)求曲线C的方程;
(2)过点F作斜率不为0的任意一条直线与曲线C交于两点A,B,试问在x轴上是否存在一点P(与点F不重合),使得∠APF=∠BPF,若存在,求出P点坐标;若不存在,说明理由.
分析 (1)设点M(x,y),利用条件可得等式$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|,化简,可得曲线C的轨迹方程;
(2)通过设存在点P(x0,0)满足题设条件,分AB与x轴不垂直与不垂直两种情况讨论,利用韦达定理化简、计算即得结论.
解答 解:(1)设点M(x,y),则据题意有$\sqrt{(x-1)^{2}+{y}^{2}}$=$\frac{1}{2}$|x-4|
则4[(x-1)2+y2]=(x-4)2,即3x2+4y2=12,∴$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
曲线C的方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)假设存在点P(x0,0)满足题设条件,
①当AB与x轴不垂直时,设AB的方程为y=k(x-1).
当AB与x轴不垂直时,设AB所在直线的方程为y=k(x-1),
代入椭圆方程化简得:(4k2+3)x2-8k2x+4k2-12=0,
可知△>0,设A(x1,y1),B(x2,y2),
则x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$,
若∠APF=∠BPF,则kAP+kBP=0,
则kAP+kBP=$\frac{{y}_{1}}{{x}_{1}-{x}_{0}}+\frac{{y}_{2}}{{x}_{2}-{x}_{0}}$=$\frac{k({x}_{1}-1)({x}_{2}-{x}_{0})+k({x}_{2}-1)({x}_{1}-{x}_{0})}{({x}_{1}-{x}_{0})({x}_{2}-{x}_{0})}$
∵(x1-1)(x2-x0)+(x2-1)(x1-x0)=2x1x2-(1+x0)(x1+x2)+2x0=0
∴整理得:k(x0-4)=0,因为k∈R,所以x0=4;
②当AB⊥x轴时,由椭圆的对称性可知恒有∠APF=∠BPF,满足题意;
综上,在x轴上存在点P(4,0),使得∠APF=∠BPF.
点评 本题考查椭圆的简单性质,圆锥曲线中的存在性问题,转化思想是解题关键,属于难题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案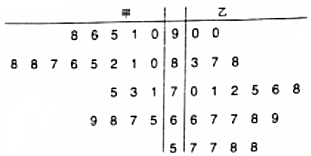
(1)现从乙班数学成绩不低于80分的同学中随机抽取两名同学,求至少有一名成绩为90分的同学被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
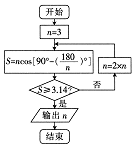 3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )
3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )