题目内容
4.若双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,则双曲线M的离心率的取值范围是( )| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
分析 由正方形的对称性得,其对称中心在原点,且在第一象限的顶点坐标为(x,x),从而得到双曲线渐近线的斜率k=$\frac{b}{a}$>1,由此能求出双曲线离心率的取值范围.
解答 解:∵双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,
∴由正方形的对称性得,其对称中心在原点,
且在第一象限的顶点坐标为(x,x),
∴双曲线渐近线的斜率k=$\frac{b}{a}$>1,
∴双曲线离心率e=$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{2}$.
∴双曲线M的离心率的取值范围是($\sqrt{2}$,+∞).
故选:A.
点评 本题考查双曲线的离心率的取值的范围的求法,是中档题,解题时要认真审题,注意双曲线性质的合理运用.

练习册系列答案
相关题目
16.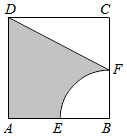 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |
17.已知命题p:?x>0,sinx>-1;q:?x>0,cosx>-1,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
13.若A={x|x2+2x-8<0},B={x|x<1},则图中阴影部分表示的集合为( )
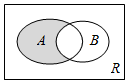

| A. | (-4,1] | B. | (1,2) | C. | [1,2) | D. | (-4,1) |
14.设集合A={-2,-1,0,1,2},集合B={y=|y=log${\;}_{\frac{1}{2}}$x,x≥1},A∩B=( )
| A. | {1,2} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {1,2,0} |