题目内容
9.已知向量$\overrightarrow a=(m,n),\overrightarrow b=(1,1)$,满足$\overrightarrow a•\overrightarrow b≥$2,且$\overrightarrow a(\overrightarrow a-2\overrightarrow b)≤0$,则$\overrightarrow a•\overrightarrow b$的取值范围是[2,4].分析 先求出$\overrightarrow{a}-2\overrightarrow{b}=(m-2,n-2)$,从而由$\overrightarrow{a}•(\overrightarrow{a}-2\overrightarrow{b})≤0$便可得到(m-1)2+(n-1)2≤2,这样便可设m-1=tcosθ,n-1=tsinθ,且$0≤t≤\sqrt{2}$,从而有$m+n=\sqrt{2}tsin(θ+\frac{π}{4})+2$,这便可得到0≤m+n≤4,从而$0≤\overrightarrow{a}•\overrightarrow{b}≤4$,再根据$\overrightarrow{a}•\overrightarrow{b}≥2$便可得出$\overrightarrow{a}•\overrightarrow{b}$的取值范围.
解答 解:$\overrightarrow{a}-2\overrightarrow{b}=(m-2,n-2)$;
由$\overrightarrow{a}•(\overrightarrow{a}-2\overrightarrow{b})≤0$得,m(m-2)+n(n-2)≤0;
∴(m-1)2+(n-1)2≤2;
∴设m-1=tcosθ,n-1=tsinθ,$0≤t≤\sqrt{2}$;
∴$m+n=t(sinθ+cosθ)+2=\sqrt{2}tsin(θ+\frac{π}{4})+2$;
$-2≤\sqrt{2}tsin(θ+\frac{π}{4})≤2$;
∴0≤m+n≤4;
又$\overrightarrow{m}•\overrightarrow{n}=m+n$,$\overrightarrow{a}•\overrightarrow{b}≥2$;
∴$2≤\overrightarrow{a}•\overrightarrow{b}≤4$;
∴$\overrightarrow{a}•\overrightarrow{b}$的取值范围是[2,4].
故答案为:[2,4].
点评 考查向量减法和数乘的坐标运算,以及数量积的坐标运算,cos2θ+sin2θ=1的运用,圆的标准方程和参数方程的转换,以及正弦函数的最值.

| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{5}$ |
| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
| A. | 3n(2n-1) | B. | 3n(2n+1) | C. | $\frac{3n(n+1)}{2}$ | D. | $\frac{3n(n-1)}{2}$ |
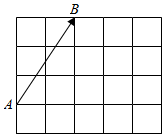 如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.
如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.