题目内容
1.已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,且满足3$\overrightarrow{a}$$+m\overrightarrow{b}$$+7\overrightarrow{c}$=$\overrightarrow{0}$,其中$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,则实数m=5或-8.分析 用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{c}$,两边平方得到关于m的方程.
解答 解:∵3$\overrightarrow{a}$$+m\overrightarrow{b}$$+7\overrightarrow{c}$=$\overrightarrow{0}$,∴-7$\overrightarrow{c}$=3$\overrightarrow{a}$+m$\overrightarrow{b}$,
∴49${\overrightarrow{c}}^{2}$=9${\overrightarrow{a}}^{2}$+m2${\overrightarrow{b}}^{2}$+6m$\overrightarrow{a}•\overrightarrow{b}$,
∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=cos60°=$\frac{1}{2}$.
∴49=9+m2+3m,
解得m=5或m=-8.
故答案为:5或-8.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
16.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y≤8}\\{2x+y≤8}\\{x≥0}\\{y≥0}\end{array}\right.$ 则目标函数z=6x+2y-1的最大值为( )
| A. | 17 | B. | 20 | C. | 21 | D. | 23 |
4.若双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,则双曲线M的离心率的取值范围是( )
| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
9.若集合A={0,1,2,4},B={1,2,3},则A∪B=( )
| A. | {1,2} | B. | {0,3,4} | C. | {0,1,2,3,4} | D. | {0,1,1,2,2,3,4} |
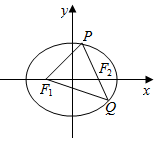 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.