题目内容
在同一平面直角坐标系中,曲线C:x2+y2=1经过伸缩变换
后,变为曲线C′.
(1)求曲线C′的方程;
(2)求曲线C′上的点到直线x+2y-8=0距离的最小值.
|
(1)求曲线C′的方程;
(2)求曲线C′上的点到直线x+2y-8=0距离的最小值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)由条件可得曲线C′的方程为:(
)2+(
)2=1,化简可得结果.
(2)根据椭圆的参数方程为
,可设点M的坐标为 (3cosθ,2sinθ).求得点M到直线的距离为d=
=
,根据余弦函数的值域求得d的最小值.
| x′ |
| 3 |
| y′ |
| 2 |
(2)根据椭圆的参数方程为
|
| |3cosθ+4sinθ-8| | ||
|
| |5cos(θ-α)-8| | ||
|
解答:
解:(1)由x2+y2=1、
,可得曲线C′的方程为:(
)2+(
)2=1,
化简得:
+
=1.
(2)因为椭圆的参数方程为
(θ为参数),
所以可设点M的坐标为 (3cosθ,2sinθ).
由点到直线的距离公式,得到点M到直线的距离为d=
=
,
由三角函数性质知,当 θ-α=0时,d取最小值为
.
|
| x′ |
| 3 |
| y′ |
| 2 |
化简得:
| x′2 |
| 9 |
| y′2 |
| 4 |
(2)因为椭圆的参数方程为
|
所以可设点M的坐标为 (3cosθ,2sinθ).
由点到直线的距离公式,得到点M到直线的距离为d=
| |3cosθ+4sinθ-8| | ||
|
| |5cos(θ-α)-8| | ||
|
由三角函数性质知,当 θ-α=0时,d取最小值为
3
| ||
| 5 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,余弦函数的值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,则输出的结果可以是( )


| A、2lnx |
| B、cosx |
| C、x-2 |
| D、e|x| |
已知直线l1与直线l2垂直,直线l1的方程为:
x-y+4=0,直线l2的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知等差数列{an}满足a2+a5=a3+ak,则整数k的值是( )
| A、2 | B、3 | C、4 | D、5 |
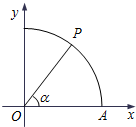 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.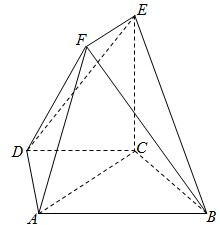 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=