题目内容
已知函数f（x）=ax2-4x+c（a，c∈R），满足f（2）=9，f（c）＜a，且函数f（x）的值域为[0，+∞）．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设函数g（x）=
（k∈R），对任意x∈[1，2]，存在x0∈[-1，1]，使得g（x）＜f（x0）求k的取值范围．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设函数g（x）=
| f(x)+kx-3 |
| x |
考点：二次函数的性质
专题：函数的性质及应用
分析：（Ⅰ）根据f（2）=9，可得4a+c=17．由判别式△=0，可得ac=4．又f（c）＜a，可得c＜a，解得a和c的值，可得 f（x）的解析式．
（Ⅱ）当x∈[-1，1]时，f（x）∈[0，9]，由题意可得g（x）=
＜9，即4x2+（k-13）x-2＜0对任意x∈[1，2]恒成立．设h（x）=4x2+（k-13）x-2，则
，由此求得k的范围．
（Ⅱ）当x∈[-1，1]时，f（x）∈[0，9]，由题意可得g（x）=
| 4x2-4x+1+kx-3 |
| x |
|
解答：
解：（Ⅰ）根据f（2）=9，可得4a+c=17．
由函数f（x）的值域为[0，+∞）知，方程ax2-4x+c=0，判别式△=0，即 ac=4．
又f（c）＜a，∴ac2-4c+c＜a，即c＜a，
解得：a=4，c=1，∴f（x）=4x2-4x+1．
（Ⅱ）当x∈[-1，1]时，f（x）∈[0，9]，
对任意x∈[1，2]，存在x0∈[-1，1]，使得g（x）＜f（x0），
即g（x）=
＜9，即4x2+（k-13）x-2＜0对任意x∈[1，2]恒成立．
设h（x）=4x2+（k-13）x-2，则
，即
，解得k＜6．
∴k的取值范围是（-∞，6）
由函数f（x）的值域为[0，+∞）知，方程ax2-4x+c=0，判别式△=0，即 ac=4．
又f（c）＜a，∴ac2-4c+c＜a，即c＜a，
解得：a=4，c=1，∴f（x）=4x2-4x+1．
（Ⅱ）当x∈[-1，1]时，f（x）∈[0，9]，
对任意x∈[1，2]，存在x0∈[-1，1]，使得g（x）＜f（x0），
即g（x）=
| 4x2-4x+1+kx-3 |
| x |
设h（x）=4x2+（k-13）x-2，则
|
|
∴k的取值范围是（-∞，6）
点评：本题主要考查二次函数的性质、函数的恒成立问题，属于基础题．
练习册系列答案
相关题目
对于等式：cos4x=cos3x+cosx，下列说法正确的是（ ）
| A、对于任意x∈R，等式都成立 |
| B、对于任意x∈R，等式都不成立 |
| C、存在无穷多个x∈R使等式成立 |
| D、等式只对有限多个x∈R成立 |
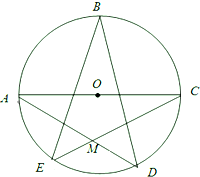如图，已知A，B，C，D，E均在⊙O上，且AC为⊙O的直径．
已知四边形ABCD是菱形，四边形BDEF是正方形，平面BDEF⊥平面ABCD，G、H、M分别是CE、CF、FB的中点．