题目内容
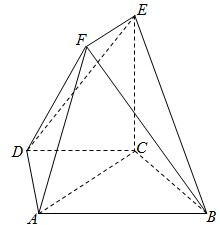 如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
(Ⅰ)求证:BC⊥AF;
(Ⅱ)若直线DE与平面ACEF所成的角的正切值是
| 1 |
| 3 |
考点:异面直线及其所成的角,平面与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AB得中点H,连CH,由题意知四边形ADCH为菱形,从而昨到△ACB为直角三角形,BC⊥AC,进而得到BC⊥平面ACEF,由此能证明BC⊥AF.
(Ⅱ)连结DH,交AC于MD,再连结EM、FM.由题意知四边形ADCH为菱形,由已知条件推导出∠DEM即为直线DE与平面ACEF所成的角,由此能求出∠FAC的余弦值.
(Ⅱ)连结DH,交AC于MD,再连结EM、FM.由题意知四边形ADCH为菱形,由已知条件推导出∠DEM即为直线DE与平面ACEF所成的角,由此能求出∠FAC的余弦值.
解答:
(Ⅰ)证明:在等腰梯形ABCD中,
∵AD=DC=CB=
AB,∴AD、BC为腰,
取AB得中点H,连CH,由题意知四边形ADCH为菱形,
则CH=AH=BH,故△ACB为直角三角形,∴BC⊥AC,…(3分)
∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF,∵AF?平面ACEF,故BC⊥AF. …(6分)
(Ⅱ)解:连结DH,交AC于MD,再连结EM、FM.由题意知四边形ADCH为菱形,
∴DM⊥AC,∵平面ACEF⊥平面ABCD,∴DM⊥平面ACEF.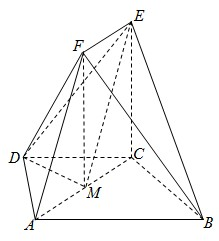
∴∠DEM即为直线DE与平面ACEF所成的角.…(9分)
设AD=DC=BC=a,则MD=
a,MC=
a
依题意,tan∠DEM=
=
∴ME=
a
在Rt△ECM中,cos∠EMC=
=
=
,
∵EF
AC=AM,∴四边形AMEF为平行四边形,
∴ME∥AF,∴∠FAC=∠EMC,
∴cos∠FAC=cos∠EMC=
.…(12分)
∵AD=DC=CB=
| 1 |
| 2 |
取AB得中点H,连CH,由题意知四边形ADCH为菱形,
则CH=AH=BH,故△ACB为直角三角形,∴BC⊥AC,…(3分)
∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF,∵AF?平面ACEF,故BC⊥AF. …(6分)
(Ⅱ)解:连结DH,交AC于MD,再连结EM、FM.由题意知四边形ADCH为菱形,
∴DM⊥AC,∵平面ACEF⊥平面ABCD,∴DM⊥平面ACEF.

∴∠DEM即为直线DE与平面ACEF所成的角.…(9分)
设AD=DC=BC=a,则MD=
| 1 |
| 2 |
| ||
| 2 |
依题意,tan∠DEM=
| DM |
| EM |
| 1 |
| 3 |
| 3 |
| 2 |
在Rt△ECM中,cos∠EMC=
| MC |
| ME |
=
| ||||
|
| ||
| 3 |
∵EF
| ||
. |
| 1 |
| 2 |
∴ME∥AF,∴∠FAC=∠EMC,
∴cos∠FAC=cos∠EMC=
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
观察数列;-4,0,4,1,-4,0,4,1,-4,0,4,1…,则a2014=( )
| A、-4 | B、0 | C、4 | D、1 |
已知数列数列{an}是等差数列,a3+a5+a7=21,求a5=( )
| A、5 | B、6 | C、7 | D、8 |
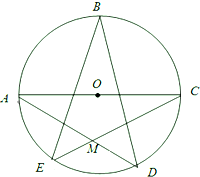 如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.
如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径. 已知四边形ABCD是菱形,四边形BDEF是正方形,平面BDEF⊥平面ABCD,G、H、M分别是CE、CF、FB的中点.
已知四边形ABCD是菱形,四边形BDEF是正方形,平面BDEF⊥平面ABCD,G、H、M分别是CE、CF、FB的中点.