题目内容
某研究性学习小组有6名同学.
(1)这6名同学排成一排,有多少种排法?
(2)若6名同学站成一排,其中甲乙两人站在最中间,有多少种排法?
(1)这6名同学排成一排,有多少种排法?
(2)若6名同学站成一排,其中甲乙两人站在最中间,有多少种排法?
考点:计数原理的应用
专题:排列组合
分析:(1)本题就是一个全排列的问题,由元素的个数可得.
(2)分两步,第一步:先确定中间甲乙两人的顺序,第二步:剩下的4名同学进行全排列,根据分步计数原理可得.
(2)分两步,第一步:先确定中间甲乙两人的顺序,第二步:剩下的4名同学进行全排列,根据分步计数原理可得.
解答:
解:(1),这6名同学排成一排,即六个元素的全排列
=720,
(2)第一步:先确定中间甲乙两人的顺序,有
种排法;
第二步:剩下的4名同学进行全排列,有
种排法,
根据分步计数原理:
=48(种)
| A | 6 6 |
(2)第一步:先确定中间甲乙两人的顺序,有
| A | 2 2 |
第二步:剩下的4名同学进行全排列,有
| A | 4 4 |
根据分步计数原理:
| A | 2 2 |
| •A | 4 4 |
点评:本题主要考查了分步计数原理,关键是如何分步,属于基础题.

练习册系列答案
相关题目
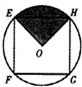 如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )
如图,EFGH是以O为圆心,1为半径的圆的内接正方形,将一颗豆子随机地掷到圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形HOE(阴影部分)内”,则P(B|A)=( )A、
| ||
B、
| ||
C、
| ||
D、
|
计算sin(-960°)的值为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
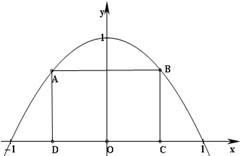 如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.