题目内容
12.在复平面xOy内,若A(2,-1),B(0,3),则?OACB中,点C对应的复数为( )| A. | 2+2i | B. | 2-2i | C. | 1+i | D. | 1-i |
分析 设C(x,y),由O(0,0),A(2,-1),B(0,3),可得$\overrightarrow{OB}、\overrightarrow{AC}$,结合OACB为平行四边形列式求得复数z.
解答 解:如图,设C(x,y),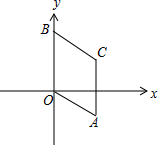
∵O(0,0),A(2,-1),B(0,3),
∴$\overrightarrow{OB}=(0,3)$,$\overrightarrow{AC}=(x-2,y+1)$,
由题意可得$\overrightarrow{OB}=\overrightarrow{AC}$,即$\left\{\begin{array}{l}{x-2=0}\\{y+1=3}\end{array}\right.$,解得x=y=2.
∴复数z=2+2i.
故选:A.
点评 本题考查复数的性质和应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在△ABC中,角A,B,C所对应的边长分别为a,b,c,面积为S,若S+a2=(b+c)2,则tanA=( )
| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |
3.由表格中的数据可以判定函数f(x)=lnx-x+2的一个零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
| x | 1 | 2 | 3 | 4 | 5 |
| lnx | 0 | 0.69 | 1.10 | 1.39 | 1.61 |
| x-2 | -1 | 0 | 1 | 2 | 3 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.直线$\left\{\begin{array}{l}x=1-\frac{1}{2}t\\ y=-3\sqrt{3}+\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t为参数)和圆x2+y2=16交于A,B两点,则AB的中点坐标为( )
| A. | (3,-3) | B. | $(-\sqrt{3},3)$ | C. | $(\sqrt{3},-3)$ | D. | (-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$) |
4.某几何体的三视图如图所示,则该几何体的表面积为( )
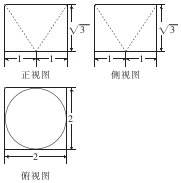

| A. | 8($\sqrt{3}$+1)+π | B. | 8($\sqrt{3}$+1)+2π | C. | 8($\sqrt{3}$+1)一π | D. | 8($\sqrt{3}$+l) |