题目内容
16．
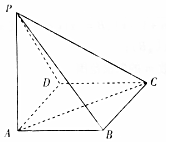如图，在底面为正方形的四棱锥P-ABCD中，侧面PAD⊥底面ABCD，PA⊥AD，PA=AD，则异面直线PB与AC所成的角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 由已知可得：PA⊥平面ABCD，底面ABCD为正方形，分别过P，D点作AD，AP的平行线交于M，连接CM，AM，因为PB∥CM，所以ACM就是异面直线PB与AC所成的角
解答 解：由题意：底面ABCD为正方形，PA⊥平面ABCD，
分别过P，D点作AD，AP的平行线交于M，连接CM，AM，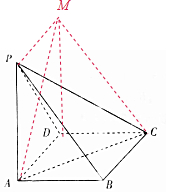
∵PM∥AD，AD∥BC，PM=AD，AD=BC．
∴PBCM是平行四边形，
∴PB∥CM，
所以∠ACM就是异面直线PB与AC所成的角．
设PA=AB=a，在三角形ACM中，AM=$\sqrt{2}$a，AC=$\sqrt{2}$a，CM=$\sqrt{2}$a
∴三角形ACM是等边三角形．
所以∠ACM等于60°，即异面直线PB与AC所成的角为60°．
故选：C
点评 本题考查了两条异面直线所成的角的证明及求法，空间直线与直线的位置关系，难度中档．
练习册系列答案
相关题目
16．已知函数f（x）=$\frac{x}{{e}^{x}}$，则f′（x）=（ ）
| A． | $\frac{x-1}{{e}^{x}}$ | B． | $\frac{x+1}{{e}^{x}}$ | C． | $\frac{-x-1}{{e}^{x}}$ | D． | $\frac{1-x}{{e}^{x}}$ |
17．已知抛物线C：x2=2y的焦点为F，A（x0，y0）是C上一点，|AF|=$\frac{5}{4}{y_0}$，则x0=（ ）
| A． | 1 | B． | -1或1 | C． | 2 | D． | -2或2 |
11．已知正方形ABCD的边长为2，H是边DA的中点，在正方形ABCD内部随机取一点P，则满足|PH|＜$\sqrt{2}$的概率为（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{8}+\frac{1}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{4}+\frac{1}{4}$ |
1．已知sinθ+cosθ=2sinα，sin2θ=2sin2β，则（ ）
| A． | cosβ=2cosα | B． | cos2β=2cos2α | C． | cos2β=2cos2α | D． | cos2β=-2cos2α |
8．已知$\overrightarrow{AB}$=（cos23°，cos67°），$\overrightarrow{BC}$=（2cos68°，2cos22°），则△ABC的面积为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 1 | D． | $\frac{\sqrt{2}}{2}$ |
6．直线$\sqrt{3}x+y-a=0$的倾斜角为（ ）
| A． | 30° | B． | 150° | C． | 60° | D． | 120° |