题目内容
如图，四棱锥P-ABCD的底面ABCD是平行四边形，PA⊥底面ABCD，PA=3，AD=2，AB=4，∠ABC=60°．（1）求证：AD⊥PC；
（2）E是侧棱PB上一点，记
| PE |
| PB |
考点：直线与平面垂直的性质,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）连接AC，分别求得AC，PC，PB，利用勾股定理证明出PC⊥BC，继而根据BC∥AD，证明出AD⊥PC．
（2）作DF⊥PC与F，作FE∥BC，交PB于E，连接AE，根据线面垂直的判定定理可证明出PC⊥平面ADE，求得PD，利用余弦定理求得cos∠PDC的值，则sin∠PDC可得，利用三角形面积公式求得三角形PDC的面积进而求得其高DF，利用勾股定理求得PF，最后于PB相比，即可求得PE；PB的值，则λ可得．
（2）作DF⊥PC与F，作FE∥BC，交PB于E，连接AE，根据线面垂直的判定定理可证明出PC⊥平面ADE，求得PD，利用余弦定理求得cos∠PDC的值，则sin∠PDC可得，利用三角形面积公式求得三角形PDC的面积进而求得其高DF，利用勾股定理求得PF，最后于PB相比，即可求得PE；PB的值，则λ可得．
解答：
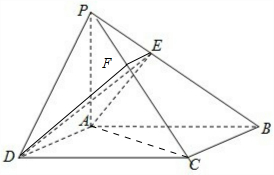（1）连接AC，
AC=
=
=2
，
∴PC=
=
=
，
∵PB=
=
=5，
∴PC2+BC2=PB2，
∴PC⊥BC，
∵BC∥AD，
∴AD⊥PC．
（2）存在，
作DF⊥PC与F，作FE∥BC，交PB于E，连接AE，
∵AD⊥PC，DF?平面ADE，AD?平面ADE，AD∩DF=D，
∴PC⊥平面ADE，
PD=
=
，PC=
，CD=AB=4，
∴在△PDC中，cos∠PDC=
=
，
∴sin∠PDC=
=
，
∴S△PDC=
PD•DC•sin∠PDC=
×4×
=4
，
∴DF=
=
=
，
∴PF=
=
=
，
∴
=
=
，
∵EF∥BC，
∴
=
=
．
∴λ=
．
（1）连接AC，AC=
| AB2+BC2-2AB•BCcos60° |
16+4-2×4×2×
|
| 3 |
∴PC=
| AC2+PA2 |
| 12+9 |
| 21 |
∵PB=
| AB2+PA2 |
| 16+9 |
∴PC2+BC2=PB2，
∴PC⊥BC，
∵BC∥AD，
∴AD⊥PC．
（2）存在，
作DF⊥PC与F，作FE∥BC，交PB于E，连接AE，
∵AD⊥PC，DF?平面ADE，AD?平面ADE，AD∩DF=D，
∴PC⊥平面ADE，
PD=
| PA2+AD2 |
| 13 |
| 21 |
∴在△PDC中，cos∠PDC=
| 13+16-21 | ||
2×
|
| ||
| 13 |
∴sin∠PDC=
1-
|
2
| ||
|
∴S△PDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
2
| ||
|
| 3 |
∴DF=
| 2S△PDC |
| PC |
8
| ||
|
8
| ||
| 7 |
∴PF=
| PD2-DF2 |
13-
|
3
| ||
| 7 |
∴
| PF |
| PC |
3
| ||
7×
|
| 3 |
| 7 |
∵EF∥BC，
∴
| PE |
| PB |
| PF |
| PC |
| 3 |
| 7 |
∴λ=
| 3 |
| 7 |
点评：本题主要考查了线面垂直的判定定理的应用．考查了学生空间观察的能力和逻辑思维能力．
练习册系列答案
相关题目