题目内容
10．已知函数f（x）=xlnx+3x-2，射线l：y=kx-k（x≥1）．若射线l恒在函数y=f（x）图象的下方，则整数k的最大值为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 由题意得问题等价于k＜$\frac{xlnx+3x-2}{x-1}$对任意x＞1恒成立，令g（x）=$\frac{xlnx+3x-2}{x-1}$，利用导数求得函数的最小值即可得出结论．
解答 解：由题意，问题等价于k＜$\frac{xlnx+3x-2}{x-1}$对任意x＞1恒成立．
令g（x）=$\frac{xlnx+3x-2}{x-1}$，∴g′（x）=$\frac{x-2-lnx}{（x-1）^{2}}$，
令h（x）=x-2-lnx，故h（x）在（1，+∞）上是增函数，
由于h（3）=1-ln3＜0，h（4）=2-ln4＞0
所以存在x0∈（3，4），使得h（x0）=x0-2-lnx0=0．
则x∈（1，x0）时，h（x）＜0；x∈（x0，+∞）时，h（x）＞0，
即x∈（1，x0）时，g'（x）＜0；x∈（x0，+∞）时，g'（x）＞0
知g（x）在（1，x0）递减，（x0，+∞）递增，
又g（x0）＜g（3）=$\frac{3}{2}$ln3+$\frac{7}{2}$＜g（4）=4+2ln4，所以kmax=5．
故选B．
点评 本题主要考查利用导数研究函数单调性、最值等性质，考查学生的运算能力，综合性较强，属于中档题．
练习册系列答案
相关题目
20．已知F为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点，l1，l2为C的两条渐近线，点A在l1上，且FA⊥l1，点B在l2上，且FB∥l1，若|FA|=$\frac{4}{5}$|FB|，则双曲线C的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | B． | $\frac{{\sqrt{5}}}{2}$或$\frac{{3\sqrt{5}}}{2}$ | C． | $\frac{{\sqrt{5}}}{2}$ | D． | $\sqrt{5}$ |
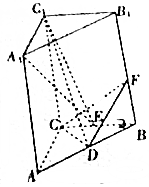如图，三棱柱ABC-A1B1C1中，CC1⊥平面ABC，∠ACB=90°，BB1=3，AC=BC=2，D，E分别为AB，BC的中点，F为BB1上一点，且$\frac{BF}{F{B}_{1}}$=$\frac{2}{7}$．