题目内容
15.函数y=tanx-1的定义域为$\left\{{x\left|{x≠\frac{π}{2}+kπ,k∈z}\right.}\right\}$.分析 根据正切函数的性质求出函数的定义域即可.
解答 解:由题意得:x≠kπ+$\frac{π}{2}$,k∈z,
故函数的定义域是:$\left\{{x\left|{x≠\frac{π}{2}+kπ,k∈z}\right.}\right\}$,
故答案为:$\left\{{x\left|{x≠\frac{π}{2}+kπ,k∈z}\right.}\right\}$.
点评 本题考查了求函数的定义域问题,考查正切函数的性质,是一道基础题.

练习册系列答案
相关题目
20.设a,b,c的平均数为M,a与b的平均数为N,N与c的平均数为P,若a>b>c,则M与P的大小关系是( )
| A. | M=P | B. | M>P | C. | M<P | D. | 不能确定 |
14.如图所示的程序框图,若输入m=8,n=3,则输出的S值为( )
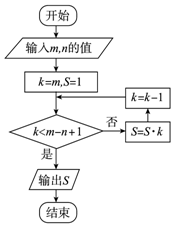

| A. | 56 | B. | 336 | C. | 360 | D. | 1440 |
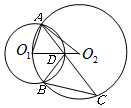 如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.
如图,已知⊙O1、⊙O2的半径分别为r1、r2,⊙O2经过点O1,且两圆相交于点A、B,C为⊙O2上的点,连接AC交⊙O1于点D,再连接BC、BD、AO1、AO2、O1O2有如下四个结论:①∠BDC=∠AO1O2;②$\frac{BD}{BC}$=$\frac{{r}_{1}}{{r}_{2}}$③AD=DC ④BC=DC,其中正确结论的序号为①②④.