题目内容
11.如果关于x的不等式|x-3|+|x-4|<a的解集不是空集,则参数a的取值范围是( )| A. | (-∞,1) | B. | (1,+∞) | C. | [1,+∞) | D. | (-∞,1] |
分析 令f(x)=|x-3|+|x-4|,可求得f(x)min=1,从而可求得参数a的取值范围.
解答 解:令f(x)=|x-3|+|x-4|,
由其几何意义(数轴上距离坐标为3的A点与坐标为4的B点的两点间的距离之和)可知,
当动点P位于A,B之间时,f(x)min=1,
∴要使关于x的不等式|x-3|+|x-4|<a的解集不是空集,
须a>1,
故选:B.
点评 本题考查绝对值不等式,利用绝对值不等式的几何意义即可求得f(x)min是关键,考查理解与运算能力,属于中档题.

练习册系列答案
相关题目
2.已知函数$f(x)=\left\{\begin{array}{l}{-2,0<x<1}\\{1,x≥1}\end{array}\right.$则不等式$lo{g}_{2}x-(lo{g}_{\frac{1}{4}}4x-1)f(lo{g}_{3}x+1)≤5$的解集为( )
| A. | ($\frac{1}{3}$,1) | B. | [1,4] | C. | ($\frac{1}{3}$,4] | D. | [1,+∞) |
19.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
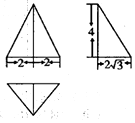
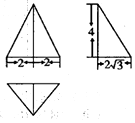
| A. | $\frac{{64\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
16.下列函数中,在(0,2)上为增函数的是( )
| A. | y=-3x+2 | B. | y=$\frac{3}{x}$ | C. | y=x2-4x+5 | D. | y=3x2+8x-10 |
3.i是虚数单位,若Z(1+i)=i,则|Z|=( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |