题目内容
1.某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.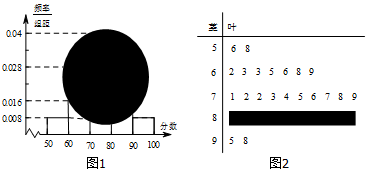
(1)求全班人数及分数在[80,90)之间的频数,并估计该班的平均分数;
(2)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
分析 (1)由茎叶图,利用频数、频率与样本容量的关系求出全班人数,计算该班的平均分;
(2)利用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)由茎叶图知,分数在[50,60)之间的频数为2,
频率为0.008×10=0.08,全班人数为$\frac{2}{0.08}=25$;
所以分数在[80,90)之间的频数为25-2-7-10-2=4,
分数在[50,60)之间的总分为56+58=114;
分数在[60,70)之间的总分为60×7+2+3+3+5+6+8+9=456;
分数在[70,80)之间的总分数为70×10+1+2+3+3+4+5+6+7+8+9=747;
分数在[80,90)之间的总分约为85×4=340;
分数在[90,100]之间的总分数为95+98=193;
所以,该班的平均分数为$\frac{114+456+747+340+193}{25}=74$;
(2)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),(5,6)共15个,
其中,至少有一个在[90,100]之间的基本事件有9个,
∴至少有一份分数在[90,100]之间的概率是$\frac{9}{15}=0.6$.
点评 本题考查了茎叶图与频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是综合性题目.

练习册系列答案
相关题目
11.如果关于x的不等式|x-3|+|x-4|<a的解集不是空集,则参数a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | [1,+∞) | D. | (-∞,1] |
12.为了了解培训讲座对某工厂工人生产时间(生产一个零件所用的时间,单位:分钟)的影响.从工厂随机选取了200名工人,再将这200名工人随机的分成A,B两组,每组100人.A组参加培训讲座,B组不参加.培训讲座结束后A,B两组中各工人的生产时间的调查结果分别为表1和表2.
表1:
表2
(1)甲、乙两名工人是随机抽取到的200名工人中的两人,求甲、乙分在不同组的概率;
(2)完成图3的频率分布直方图,比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小;(不用计算,可通过直方图直接回答结论)
(3)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关?
下面临界值表仅供参考:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
表1:
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) |
| 人数 | 30 | 40 | 20 | 10 |
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) |
| 人数 | 10 | 25 | 20 | 30 | 15 |
(2)完成图3的频率分布直方图,比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小;(不用计算,可通过直方图直接回答结论)

(3)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关?
| 生产时间小于70分钟 | 生产时间不小于70分钟 | 合计 | |
| A组工人 | a= | b= | |
| B组工人 | c= | d= | |
| 合计 | n= |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |