题目内容
20.已知数列{an}满足a1=1,an+1-3an=1.(1)证明:$\{{a_n}+\frac{1}{2}\}$是等比数列,并求{an}的通项公式;
(2)设bn=2nan+n,求数列{bn}的前n项和Sn.
分析 (1)由已知数列递推式可得${a_{n+1}}+\frac{1}{2}=3({a_n}+\frac{1}{2})$,进一步得到$\left\{{{a_n}+\frac{1}{2}}\right\}$是首项为$\frac{3}{2}$,公比为3的等比数列.求出等比数列的通项公式,可得{an}的通项公式;
(2)把{an}的通项公式代入bn=2nan+n,利用错位相减法求数列{bn}的前n项和Sn.
解答 证明:(1)由an+1-3an=1,得an+1=3an+1,得${a_{n+1}}+\frac{1}{2}=3({a_n}+\frac{1}{2})$,
又${a_1}+\frac{1}{2}=\frac{3}{2}$≠0,
∴$\left\{{{a_n}+\frac{1}{2}}\right\}$是首项为$\frac{3}{2}$,公比为3的等比数列.
∴${a_n}+\frac{1}{2}=\frac{3^n}{2}$,则${a}_{n}=\frac{{3}^{n}-1}{2}$.
因此{an}的通项公式为${a_n}=\frac{{{3^n}-1}}{2}$;
解:(2)由(1)得${a_n}=\frac{{{3^n}-1}}{2}$,
∴bn=2nan+n=n•3n.
Sn=1•31+2•32+3•33+…+n•3n,①
3Sn=1•32+2•33+…+(n-1)•3n+n•3n+1.②
①-②得-2Sn=31+32+…+3n-n•3n+1
=$\frac{3(1-{3}^{n})}{1-3}$-n•3n+1=$\frac{{3}^{n+1}-3}{2}-n•{3}^{n+1}$.
∴Sn=$\frac{(2n-1)•{3}^{n+1}+3}{4}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,是中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | (-∞,1) | B. | (1,+∞) | C. | [1,+∞) | D. | (-∞,1] |
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
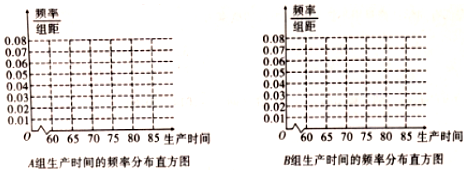
表1:
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) |
| 人数 | 30 | 40 | 20 | 10 |
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) |
| 人数 | 10 | 25 | 20 | 30 | 15 |
(2)完成图3的频率分布直方图,比较两组的生产时间的中位数的大小和两组工人中个体间的差异程度的大小;(不用计算,可通过直方图直接回答结论)
(3)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产时间”与参加培训讲座有关?
| 生产时间小于70分钟 | 生产时间不小于70分钟 | 合计 | |
| A组工人 | a= | b= | |
| B组工人 | c= | d= | |
| 合计 | n= |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 如图,在△ABC中,内角A、B、C所对的边分别是a、b、c,$B=\frac{π}{3}$,a=2.
如图,在△ABC中,内角A、B、C所对的边分别是a、b、c,$B=\frac{π}{3}$,a=2.