题目内容
有七名同学站成一排照毕业纪念照，其中甲不能和乙站在一起，并且乙、丙两位同学要站在一起，则不同的站法有 种．
考点：排列、组合的实际应用
专题：应用题,排列组合
分析：先排除甲的其余6人，因为乙、丙两位同学要站在一起，故捆绑再与其余5人进行全排，再将甲插空，由于甲不能和乙站在一起，故甲有5种插法，根据乘法原理即可得到结论．
解答：
解：根据题意，先排除甲的其余6人，因为乙、丙两位同学要站在一起，故捆绑再与其余5人进行全排，
共有
=240种排法，
再将甲插空，由于甲不能和乙站在一起，
故甲有5种插法，所以根据乘法原理，不同的站法有240×5=1200种．
故答案为：1200．
共有
| A | 5 5 |
| A | 2 2 |
再将甲插空，由于甲不能和乙站在一起，
故甲有5种插法，所以根据乘法原理，不同的站法有240×5=1200种．
故答案为：1200．
点评：本题考查排列知识，考查乘法原理的运用，考查学生分析解决问题的能力．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，已知曲线C由圆弧C1和圆弧C2相接而成，两相接点M、N均在直线x=6上，圆弧C1的圆心是坐标原点O，半径为10，圆弧C2过点A（38，0）．
某校高三年级有500名同学，将他们的身高（单位：cm）数据绘制成频率分布直方图（如图），现用分层抽样的方法选取x名学生参加某项课外活动，已知从身高在[160，170）的学生中选取9人，则x=
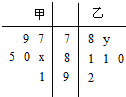某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是85，乙班学生成绩的平均分为81，则x+y的值为（ ）