题目内容
函数函数y=sin（3x+
）cos（x-
）+cos（3x+
）sin（x-
）的图象的一条对称轴的方程是（ ）
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：将三角函数进行化简，根据三角函数的图象和性质即可得到结论．
解答：
解：y=sin（3x+
）cos（x-
）+cos（3x+
）sin（x-
）=sin（3x+
+x-
）=sin（4x+
），
由4x+
=kπ+
，得x=
+
，k∈Z，
当k=0时，x=
，
故选：C．
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
由4x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 4 |
| π |
| 12 |
当k=0时，x=
| π |
| 12 |
故选：C．
点评：本题主要考查三角函数的图象和性质，利用三角公式将函数进行化简是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
、
满足|
|=1，|
|=
，且（3
-2
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某几何体的三视图，则该几何体的体积为（ ）
| A、π | ||
B、
| ||
C、
| ||
D、
|
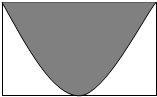如图，长方形的面积为2，将100颗豆子随机地撒在长方形内，其中恰好有60颗豆子落在阴影部分内，则用随机摸拟的方法可以估计图中阴影部分的面积为（ ）
任意画一个正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了3个正方形，如图所示．若向图形中随机投一点，则所投点落在第三个正方形的概率是（ ）