题目内容
9.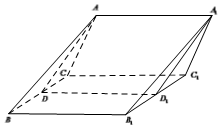 如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.
如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.(Ⅰ)求证:四边形CBB1C1为矩形;
(Ⅱ)若$∠AD{D_1}=\frac{π}{3}$,且A-BB1C1C体积为$\sqrt{3}$,求三棱柱ABC-A1B1C1的侧面积.
分析 (Ⅰ)作AO⊥DD1,证明BC⊥平面ADD1A1,即可证明四边形CBB1C1为矩形;
(Ⅱ)若$∠AD{D_1}=\frac{π}{3}$,且A-BB1C1C体积为$\sqrt{3}$,求出三棱柱ABC-A1B1C1的直截面的周长,即可求三棱柱ABC-A1B1C1的侧面积.
解答 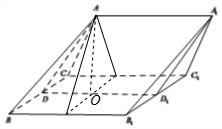 (Ⅰ)证明:作AO⊥DD1,则
(Ⅰ)证明:作AO⊥DD1,则
∵平面ADD1A1⊥平面CBB1C1,平面ADD1A1∩平面CBB1C1=DD1,∴AO⊥平面CBB1C1,
∴AO⊥BC,
∵AB=BC=CA,D是BC的中点,∴BC⊥AD,
∵AO∩AD=A,
∴BC⊥平面ADD1A1,
∴BC⊥DD1,∴BC⊥CC1,
∴四边形CBB1C1为矩形;
(Ⅱ)解:设AB=2a,则AO=$\frac{3}{2}$a,BB1=$\sqrt{3}$a,
∴A-BB1C1C体积=$\frac{1}{3}×2a×\sqrt{3}a×\frac{3}{2}a$=$\sqrt{3}$,∴a=1,
∴三棱柱ABC-A1B1C1的直截面的边长分别为2,$\sqrt{\frac{9}{4}+1}$,$\sqrt{\frac{9}{4}+1}$,
∴三棱柱ABC-A1B1C1的侧面积=(2+$\frac{\sqrt{13}}{2}$+$\frac{\sqrt{13}}{2}$)×2=4+2$\sqrt{13}$.
点评 本题考查线面垂直的判定与性质,考查三棱柱ABC-A1B1C1的侧面积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
19.复数z满足z(3i-4)=25(i是虚数单位),则z的共轭复数$\overline z$=( )
| A. | 4+3i | B. | 4-3i | C. | -4+3i | D. | -4-3i |
1.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{0}&{x=1}\\{|lg|x-1||}&{x≠1}\end{array}\right.$,则关于x的方程f2(x)+bf(x)+c=0有7个不同实数解的充要条件是( )
| A. | b<0且c>0 | B. | b>0且c<0 | C. | b<0且c=0 | D. | b>0且c=0 |
18.若两个球的体积之比为1:8,则这两个球的表面积之比为( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
19.已知a=sin$\frac{2π}{7}$,b=cos$\frac{2π}{7}$,c=tan$\frac{2π}{7}$,则( )
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
 如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.
如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.