题目内容
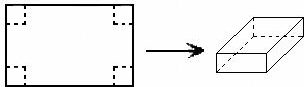
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),则该容器的高为 时,容器的容积最大?最大容积是 ?

考点:基本不等式
专题:导数的综合应用
分析:设在四角分别截去一个小正方形的边长为xcm,可得该容器的长宽分别为90-2x,(48-2x)cm.(0<x<24)该容器的容积V=(90-2x)(48-2x)x,利用导数研究其单调性极值与最值即可.
解答:
解:设在四角分别截去一个小正方形的边长为xcm,
该容器的长宽分别为90-2x,(48-2x)cm.(0<x<24)
该容器的容积V=(90-2x)(48-2x)x=4x3-276x2+4320x,
V′=12x2-552x+4320=12(x2-46x+360).
令V′=0,∵0<x<24,解得x=10.
当0<x<10时,V′>0,函数V(x)单调递增;当10<x<24时,V′<0,函数V(x)单调递减.
∴当x=10cm时,V(x)取得最大值,V(10)=19600(cm3).
故答案分别为:10cm,19600(cm3).
该容器的长宽分别为90-2x,(48-2x)cm.(0<x<24)
该容器的容积V=(90-2x)(48-2x)x=4x3-276x2+4320x,
V′=12x2-552x+4320=12(x2-46x+360).
令V′=0,∵0<x<24,解得x=10.
当0<x<10时,V′>0,函数V(x)单调递增;当10<x<24时,V′<0,函数V(x)单调递减.
∴当x=10cm时,V(x)取得最大值,V(10)=19600(cm3).
故答案分别为:10cm,19600(cm3).
点评:本题考查了长方体的体积计算公式、利用导数研究其单调性极值与最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
+
的定义域是( )
| ln(1-x) | ||
|
| 1 |
| x |
| A、[-1,0)∪(0,1) |
| B、[-1,0)∪(0,1] |
| C、(-1,0)∪(0,1] |
| D、(-1,0)∪(0,1) |
若函数f(x)=
,则函数y=f(x)-x的零点个数是( )
|
| A、0 | B、1 | C、2 | D、3 |
已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为( )
| A、27 | B、11 | C、109 | D、36 |
