题目内容
10．已知方程x2+my2=1表示焦点在y轴上的椭圆，则m的取值范围是（ ）| A． | m＜1 | B． | -1＜m＜1 | C． | m＞1 | D． | 0＜m＜1 |
分析 根据题意，将方程变形为$\frac{{y}^{2}}{\frac{1}{m}}$+$\frac{{x}^{2}}{1}$=1，由椭圆的标准方程分析可得$\frac{1}{m}$＞1，解可得m的取值范围，即可得答案．
解答 解：根据题意，方程x2+my2=1变形可得：$\frac{{y}^{2}}{\frac{1}{m}}$+$\frac{{x}^{2}}{1}$=1，
若其表示焦点在y轴上的椭圆，
则有$\frac{1}{m}$＞1，
解可得0＜m＜1；
故选：D．
点评 本题考查椭圆的标准方程，关键是掌握椭圆的标准方程的形式．
练习册系列答案
相关题目
5．“an+1an-1=an2，n≥2且n∈N”是“数列{an}为等比数列”的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
15．
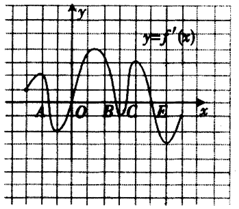函数y=f（x）定义在区间（-3，7）上，其导函数如图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是（ ）
函数y=f（x）定义在区间（-3，7）上，其导函数如图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
19．已知集合P={x|1≤x≤3}，Q={x|（x-1）2≤4}，则P∩Q=（ ）
| A． | [-1，3] | B． | [1，3] | C． | [1，2] | D． | （-∞，3] |
20．
如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB=2，AD=DC=1，图中圆弧所在圆的圆心为点C，半径为$\frac{1}{2}$，且点P在图中阴影部分（包括边界）运动．若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$，其中x，y∈R，则4x-y的最大值为（ ）
如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB=2，AD=DC=1，图中圆弧所在圆的圆心为点C，半径为$\frac{1}{2}$，且点P在图中阴影部分（包括边界）运动．若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$，其中x，y∈R，则4x-y的最大值为（ ）| A． | $3-\frac{{\sqrt{2}}}{4}$ | B． | $3+\frac{{\sqrt{5}}}{2}$ | C． | 2 | D． | $3+\;\frac{{\sqrt{17}}}{2}$ |