题目内容

18．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-x，x＞0}\\{1-|2x+1|，x≤0}\end{array}\right.$，若关于x的方程f（x）=kx-1有两个不相等的实数根，则实数k的取值范围为{k|k≥2或k=1}．

分析 作出f（x）的图象，利用数形结合建立条件关系进行求解即可．

解答 解：当x≤0时，f（x）=$\left\{\begin{array}{l}{-2x，（-\frac{1}{2}≤x≤0）}\\{2+2x，（x＜-\frac{1}{2}）}\end{array}\right.$，函数f（x）在其定义域内的图象如下：
直线l1与y=x2-x相切，联立{，$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}-x}\end{array}\right.$，消元后△=0得k=1，
即k=1时，方程f（x）=kx-1有两个不相等的实数根．
直线l2与直线l3平行时，方程f（x）=kx-1有两个不相等的实数根，
当l2绕点（0，-1）向y轴靠近，方程f（x）=kx-1有两个不相等的实数根．
实数k的取值范围为：k≥2，或k=1．
故答案为：{k|k≥2或k=1}．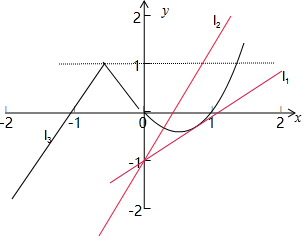

点评 本题主要考查函数与方程的应用，利用数形结合转化为两个函数的交点个数问题是解决本题的关键．

练习册系列答案
相关题目
8．已知函数$f（x）=\frac{{2-\sqrt{2}sin\frac{π}{4}x}}{{{x^2}+4x+5}}（{-4≤x≤0}）$，则f（x）的最大值为2+$\sqrt{2}$．
9．已知$|{\overrightarrow a}|=6\sqrt{3}，|{\overrightarrow b}|=\frac{1}{3}$，且$\overrightarrow a•\overrightarrow b=-3$，则$\overrightarrow a$与$\overrightarrow b$的夹角为（　　）
A．$\frac{π}{2}$B．$\frac{π}{6}$C．$\frac{π}{3}$D．$\frac{5π}{6}$
6．设抛物线$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$（t为参数，p＞0）的焦点为F（1，0），过F的直线与抛物线交于A，B两点，且满足|AF|=3|BF|，则弦AB的中点到准线的距离为$\frac{8}{3}$．
13．在平行四边形ABCD中，AB=2，BC=$\sqrt{2}$，∠DAB=45°，点E为BC的中点，$\overrightarrow{FC}$=3$\overrightarrow{DF}$，则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是（　　）
A．-1B．-$\frac{4}{3}$C．$\frac{3}{4}$D．-$\frac{3}{4}$
3．复数$\frac{5i}{1+2i}$的虚部是（　　）
A．iB．-iC．1D．-1
10．已知函数f（x）=${x^3}+f'（\frac{2}{3}）{x^2}$-x+c，（其中$f'（\frac{2}{3}）$为f（x）在点x=$\frac{2}{3}$处的导数，c为常数）．
（1）求$f'（\frac{2}{3}）$的值；
（2）求函数f（x）的单调区间；
（3）设函数g（x）=[f（x）-x3]•ex，若函数g（x）在区间[-3，2]上单调递增，求实数c的取值范围．
9．已知实数x，y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{3x-y-5≥0}\end{array}\right.$，则z=$\frac{y+1}{2x}$的最大值为$\frac{5}{6}$．
10．已知方程x2+my2=1表示焦点在y轴上的椭圆，则m的取值范围是（　　）
A．m＜1B．-1＜m＜1C．m＞1D．0＜m＜1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网