题目内容
8.下列命题中①复数a+bi与c+di相等的充要条件是a=c且b=d
②任何复数都不能比较大小
③若$\overrightarrow{{z}_{1}}$=$\overrightarrow{{z}_{2}}$,则|$\overrightarrow{{z}_{1}}$|=|$\overrightarrow{{z}_{2}}$|
④若|$\overrightarrow{{z}_{1}}$|=|$\overrightarrow{{z}_{2}}$|,则$\overrightarrow{{z}_{1}}$=$\overrightarrow{{z}_{2}}$或$\overrightarrow{{z}_{1}}$=-$\overrightarrow{{z}_{2}}$.
正确的选项是( )
| A. | ①③ | B. | ①② | C. | ①③④ | D. | ②③④ |
分析 根据复数的有关概念和定义分别进行判断即可.
解答 解:①两个复数相等,则实部相等,虚部相等,则复数a+bi与c+di相等的充要条件是a=c且b=d,正确,
②任何复数都不能比较大小,错误,当两个复数为实数时,是可以比较大小的,故②错误.
③若$\overrightarrow{{z}_{1}}$=$\overrightarrow{{z}_{2}}$,则|$\overrightarrow{{z}_{1}}$|=|$\overrightarrow{{z}_{2}}$|,正确,
④若|$\overrightarrow{{z}_{1}}$|=|$\overrightarrow{{z}_{2}}$|,则$\overrightarrow{{z}_{1}}$=$\overrightarrow{{z}_{2}}$或$\overrightarrow{{z}_{1}}$=-$\overrightarrow{{z}_{2}}$.错误,比如$\overrightarrow{{z}_{1}}$=i,$\overrightarrow{{z}_{2}}$=1,满足,|$\overrightarrow{{z}_{1}}$|=|$\overrightarrow{{z}_{2}}$|,但$\overrightarrow{{z}_{1}}$=$\overrightarrow{{z}_{2}}$或$\overrightarrow{{z}_{1}}$=-$\overrightarrow{{z}_{2}}$不成立,
故选:A
点评 本题主要考查命题的真假判断涉及复数的有关概念,模长的计算以及复数相等的判断,比较基础.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
3.实数x,y满足$\left\{\begin{array}{l}{x+y-a≤0}\\{x-y≥0}\\{y≥0}\\{\;}\end{array}\right.$,若z=x-2y的最小值为-1,则实数a的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
13.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2016×22015 | B. | 2016×22014 | C. | 2017×22015 | D. | 2017×22014 |
20.在平面直角坐标系中,“点M的坐标满足方程4$\sqrt{x}$+y=0”是“点M在曲线y2=16x上”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
18.若f(x)是定义在(-1,1)上的减函数,则下列不等式正确的是( )
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
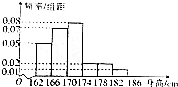 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.