Question

19．设区域Ω={（x，y）|0≤x≤1，0≤y≤1}，区域A={（x，y）|y≤$\sqrt{x}$，（x，y）∈Ω}，在区域Ω中随机取一个点，则该点在A中的概率$\frac{2}{3}$．

Answer 1

分析 首先利用定积分求出阴影部分区域面积，然后利用定积分求几何概型概率．

解答 解：如图，区域Ω对应的部分是边长为1的正方形，区域A对应部分为图中阴影部分，面积为${∫}_{0}^{1}\sqrt{x}dx=\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{1}=\frac{2}{3}$，
由几何概型公式得到在区域Ω中随机取一个点，则该点在A中的概率为$\frac{\frac{2}{3}}{1}$=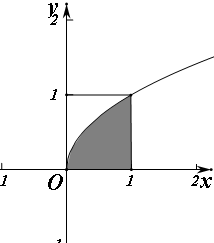$\frac{2}{3}$；
故答案为：$\frac{2}{3}$．

点评 本题考查了定积分求曲边梯形的面积以及几何概型的求法；利用面积比求概率是几何概型的概率求法中经常运用的方法．