题目内容
17.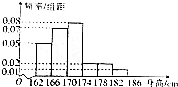 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.(1)试评估市一中高三年级参加体检的男生在全市高三年级参加体验的男生中的平均身高状况(同一组中的数据用该区间的中间值作代表);
(2)在这50名参加体检的男生身高在178cm以上(含178cm)的人中任意抽取3人,将该3人中身高排名(从高到低)在全市参加体检的高三男生身高前52名的人数记为X,求X的数学期望.
若X-N(μ,δ2),则P(μ-δ<X≤μ+δ)=0.6826,P(μ-2δ<X≤μ+2δ))=0.9544,P(μ-3δ<X≤μ+3δ)=0.9974.
分析 高三男生的平均身高用组中值×频率,即可得到结论;
先根据正态分布的规律求出全市前52名的身高在182cm以上的50人中的人数,确定X的可能取值,求出其概率,即可得到X的分布列与期望.
解答 解:由直方图,经过计算该校高三年级男生平均身高为:
164×0.05×4+168×0.07×4+17×0.08×4+176×0.02×4+18×0.02×4+184×0.01×4=170.72,
高于全市平均身高170,
(2)由男生身高在178cm以上(含178cm)的人中总共有0.12×5=6人,
∵P(170-3×4<X≤170+3×4)=0.9974.
∴P(X≥182)=$\frac{1-0.9974}{2}$=0.0013,
全省高中男生身高排名(从高到低) 前52名中最低身高是182 cm;
全省前52名的身高在182cm以上,这50人中182cm以上的有2人.
随机变量X可取0,1,2,于是:
P(X=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=0.2,
P(X=1)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=0.6,
P(X=2)=$\frac{{C}_{4}^{1}•{C}_{2}^{2}}{{C}_{6}^{3}}$=0.2;
E(X)=0×0.2+1×0.6+2×0.2=1.
点评 此题主要考查了正态分布,考查随机变量的定义及其分布列,并考查了利用分布列求其期望.正确理解频数分布直方图横纵轴表示的意义,由频数分布直方图可以得到什么结论是学习中需要掌握的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设a=${(\frac{1}{2})^{\frac{1}{2}}}$,b=log20142015,c=log42,则( )
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | a>c>b |
5.已知数列{an}的前n项为Sn,且满足关系式lg(Sn-1)=n (n∈N*),则数列{an}的通项公式an=( )
| A. | 9•10n-1 | B. | $\left\{{\begin{array}{l}{11}\\{9•{{10}^{n-1}}}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ | ||
| C. | 10n+1 | D. | $\left\{{\begin{array}{l}9\\{{{10}^n}+1}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ |
7.已知数列{an}满足an+1=$\sqrt{{a}_{n}^{2}-2{a}_{n}+2}$+1(n∈N*),则使不等式a2016>2016成立的所有正整数a1的集合为( )
| A. | {a1|a1≥2016,a1∈N*} | B. | {a1|a1≥2015,a1∈N*} | C. | {a1|a1≥2014,a1∈N*} | D. | {a1|a1≥2013,a1∈N*} |