Question

3．实数x，y满足$\left\{\begin{array}{l}{x+y-a≤0}\\{x-y≥0}\\{y≥0}\\{\;}\end{array}\right.$，若z=x-2y的最小值为-1，则实数a的值为（　　）

• A． 2
• B． 1
• C． 0
• D． -1

Answer 1

分析 画出满足条件的平面区域，求出角点的坐标，结合函数的图象求出a的值即可．

解答 解：画出满足条件的平面区域，如图示：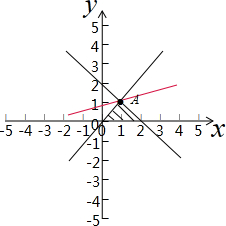
，
由$\left\{\begin{array}{l}{x+y-a=0}\\{x-y=0}\end{array}\right.$，解得A（$\frac{a}{2}$，$\frac{a}{2}$），
由z=x-2y得：y=$\frac{1}{2}$x-$\frac{z}{2}$，
平移直线y=$\frac{1}{2}$x，
显然直线过A时，z最小，z的最小值是z=$\frac{a}{2}$-a=-1，
解得：a=2，
故选：A．

点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道中∝档题．