题目内容
3.已知不等式$({x+y})({\frac{1}{x}+\frac{a}{y}})≥9$对于任意xy>0恒成立,求正实数a的范围a≥4.分析 首先分析题目已知不等式对任意x、y的正实数恒成立.故对不等式左边展开后,利用基本不等式得恒成立的满足条件($\sqrt{a}$+1)2≥9,然后解不等式,可求a值
解答 解:因为(x+y)($\frac{1}{x}$+$\frac{a}{y}$)=1+a+$\frac{y}{x}$+$\frac{ax}{y}$≥1+a+2$\sqrt{\frac{y}{x}•\frac{ax}{y}}$=1+a+2$\sqrt{a}$=($\sqrt{a}$+1)2,a>0,
要使原不等式恒成立,则只需($\sqrt{a}$+1)2≥9,
即$\sqrt{a}$+1≥3,
解得a≥4,
故答案为:a≥4.
点评 此题主要考查基本不等式的应用,在利用基本不等式求参数的值或范围时,只需求出式子的最小值或最大值,使其满足已知条件即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知函数f(x)=2x-$\frac{x^2}{π}$+cosx,设x1,x2∈(0,π),x1≠x2,且f(x1)=f(x2),若x1,x0,x2成等差数列,则( )
| A. | f'(x0)>0 | B. | f'(x0)=0 | ||
| C. | f'(x0)<0 | D. | f'(x0)的符号不能确定 |
14.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
15.对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+$\sqrt{x-1}$是“Kobe函数”,则实数k的取值范围是( )
| A. | [-1,0] | B. | [1,+∞) | C. | $[{-1,-\frac{3}{4}})$ | D. | $({\frac{3}{4},1}]$ |
12.函数y=x-ex的增区间为( )
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,1) |
13.已知函数f(x)是定义在R上的偶函数,且在(-∞,0]上单调递减,若f(-1)=0,则不等式f(2x-1)>0解集为( B )( )
| A. | (-6,0)∪(1,3) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,1)∪(3,+∞) | D. | (-∞,-1)∪(3,+∞) |
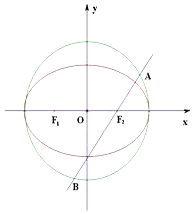 已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)
已知椭圆的标准方程为:$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{3{a}^{2}}$=1(a>0)