题目内容
若函数cosx=
,且x∈R,则m的取值范围是 .
| 2m-1 |
| 3m+2 |
考点:任意角的三角函数的定义
专题:不等式的解法及应用
分析:cosx=
∈[-1,1],可得
,解分式不等式求得它的解集.
| 2m-1 |
| 3m+2 |
|
解答:
解:由于函数cosx=
∈[-1,1],可得
,即
,
即
,求得 m≤-3,或m≥-
,
故答案为:{m|m≤-3,或m≥-
}.
| 2m-1 |
| 3m+2 |
|
|
即
|
| 1 |
| 5 |
故答案为:{m|m≤-3,或m≥-
| 1 |
| 5 |
点评:本题主要考查余弦函数的值域,分式不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知等比数列{an}的公比q<0,其前n 项的和为Sn,则a9S8与a8S9 的大小关系是( )
| A、a9S8>a8S9 |
| B、a9S8<a8S9 |
| C、a9S8≥a8S9 |
| D、a9S8≤a8S9 |
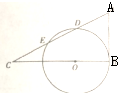 如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=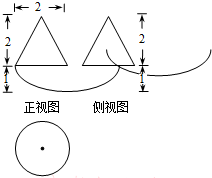
 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.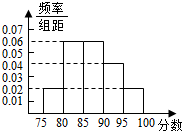 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: