题目内容
20.已知双曲线$\frac{x^2}{m-3}+\frac{y^2}{m+5}=1$的离心率为$\frac{4}{3}$,那么此双曲线的准线方程为$y=±\frac{{9\sqrt{2}}}{8}$.分析 利用双曲线$\frac{x^2}{m-3}+\frac{y^2}{m+5}=1$的离心率为$\frac{4}{3}$,求出a,c,再求出双曲线的准线方程.
解答 解:∵双曲线$\frac{x^2}{m-3}+\frac{y^2}{m+5}=1$的离心率为$\frac{4}{3}$,
∴(m-3)(m+5)<0,$\frac{c}{a}$=$\frac{4}{3}$,
∴-5<m<3,$\frac{m+5+3-m}{m+5}$=$\frac{16}{9}$,
∴m=-$\frac{1}{2}$,
∴a=$\frac{3\sqrt{2}}{2}$,c=2$\sqrt{2}$,
∴双曲线的准线方程为$y=±\frac{{9\sqrt{2}}}{8}$
故答案为:$y=±\frac{{9\sqrt{2}}}{8}$.
点评 本题考查双曲线的准线方程,考查离心率,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
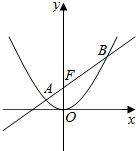 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.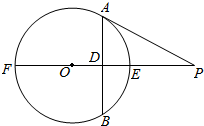 如图,已知PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,过点A作PO的垂线交⊙O于点B,垂足为D.
如图,已知PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,过点A作PO的垂线交⊙O于点B,垂足为D.