题目内容

6．命题“若x＞2，则x＞1”的逆否命题是（　　）
A．若x＜2，则x＜1B．若x≤2，则x≤1C．若x≤1，则x≤2D．若x＜1，则x＜2

分析 根据逆否命题的定义，结合已知中的原命题，可得答案．

解答 解：命题“若x＞2，则x＞1”的逆否命题是“若x≤1，则x≤2”，
故选：C

点评 本题考查的知识点是四种命题，难度不大，属于基础题．

练习册系列答案
相关题目
16．（Ⅰ）解不等式$\frac{{x}^{2}-x-6}{x-1}$＞0
（Ⅱ）设a＞0，b＞0，c＞0，且a+b+c=1，求证（$\frac{1}{a}$-1）（$\frac{1}{b}$-1）（$\frac{1}{c}$-1）≥8．
17．函数f（x）=ex与函数g（x）=-2x+3的图象的交点的横坐标所在的大致区间是（　　）
A．（-1，0）B．$（{0，\frac{1}{2}}）$C．$（{\frac{1}{2}，1}）$D．（1，2）
14．将函数f（x）=$\sqrt{3}$sinxcosx+sin2x的图象上各点的纵坐标不变，横坐标变为原来的2倍，再沿x轴向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，则y=g（x）的一个递增区间是（　　）
A．$[{-\frac{π}{6}，\frac{5π}{6}}]$B．$[{-\frac{π}{2}，\frac{π}{2}}]$C．$[{-\frac{π}{12}，\frac{4π}{3}}]$D．$[{-\frac{π}{4}，0}]$
1．甲、乙两人玩一种游戏，游戏规则如下：先将筹码放在如下表的正中间D处，投掷一枚质地均匀的硬币，若正面朝上，筹码向右移动一格；若反面朝上，筹码向左移动一格．
ABCDEFG
305101052030
（1）将硬币连续投掷三次，现约定：若筹码停在A或B或C或D处，则甲赢；否则，乙赢．问该约定对乙公平吗？请说明理由．
（2）设甲、乙两人各有100个积分，筹码停在D处，现约定：
①投掷一次硬币，甲付给乙10个积分；乙付给甲的积分数是，按照上述游戏规则筹码所在表中字母A-G下方所对应的数目；
②每次游戏筹码都连续走三步，之后重新回到起始位置D处．
你认为该规定对甲、乙二人哪一个有利，请说明理由．
11．如图，在四面体ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AC}=\overrightarrow b，\overrightarrow{AD}$=$\overrightarrow c$，点M在AB上，且AM=$\frac{2}{3}$AB，点N是CD的中点，则$\overrightarrow{MN}$=（　　）
A．$\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$B．$-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$C．$\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow c$D．$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$
18．已知空间四点A（2，0，0），B（0，2，1），C（1，1，1），D（-1，m，n）．
（1）若AB∥CD，求实数m，n的值；
（2）若m+n=1，且直线AB和CD所成角的余弦值为$\frac{1}{3}$，求实数m的值．
15．已知平面区域D=$\left\{{（{x，y}）\left|\begin{array}{l}\\ 3x+y≥3\\ x-y≤2\\ x+3y≤3\end{array}\right.}\right\}$，z=3x-2y，若命题“?（x0，y0）∈D，z＞m”为假命题，则实数m的最小值为$\frac{25}{4}$．
16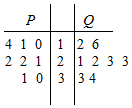．从某工厂生产的P，Q两种型号的玻璃种分别随机抽取8个样品进行检查，对其硬度系数进行统计，统计数据用茎叶图表示（如图所示），则P组数据的众数和Q组数据的中位数分别为（　　）
A．22和22.5B．21.5和23C．22和22D．21.5和22.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网