题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是边长为3的正方形,平面PCD⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为3的正方形,平面PCD⊥底面ABCD,E是PC的中点.(Ⅰ)求证:PA∥平面BDE;
(Ⅱ)若PD=PC=
| ||
| 2 |
(Ⅲ)若侧棱PD⊥底面ABCD,PD=4.求△PAD以PA为轴旋转所围成的几何体体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连接AC交BD于O,连接EO,证明OE∥PA,即可证明PA∥平面BDE;
(Ⅱ)证明PD⊥平面PCB,可得平面PDA⊥平面PCB;
(Ⅲ)过D作PA的垂线.垂足为H,则几何体为以DH为半径,分别以PH,AH为高的两个圆锥的组合体,即可求△PAD以PA为轴旋转所围成的几何体体积.
(Ⅱ)证明PD⊥平面PCB,可得平面PDA⊥平面PCB;
(Ⅲ)过D作PA的垂线.垂足为H,则几何体为以DH为半径,分别以PH,AH为高的两个圆锥的组合体,即可求△PAD以PA为轴旋转所围成的几何体体积.
解答:
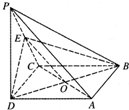 (Ⅰ)证明:连接AC交BD于O,连接EO.
(Ⅰ)证明:连接AC交BD于O,连接EO.
∵ABCD是正方形,∴O为AC中点,
∵已知E为PC的中点,
∴OE∥PA.…(2分)
又∵OE?平面BDE,PA?平面BDE,∴PA∥平面BDE.…(3分)
(Ⅱ)证明:在△DPC中,PD=PC=
DC,∴PD2+PC2=DC2,即DP⊥PC.…(4分)
又已知:平面PCD⊥底面ABCD,平面PCD∩平面ABCD=DC,BC⊥DC;
∴BC⊥平面PDC,PD?平面PDC,∴PD⊥BC,…(6分)
BC与PC相交且在平面PBC内.
∴PD⊥平面PCB,PD?平面PDA,∴平面PDA⊥平面PCB.…(8分)
(Ⅲ)解:过D作PA的垂线.垂足为H,则几何体为以DH为半径,分别以PH,AH为高的两个圆锥
的组合体.…(9分)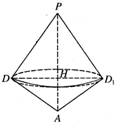
侧棱PD⊥底面ABCD,∴PD⊥DA,PD=4,DA=DC=3,∴PA=5
DH=
=
=
,…(10分
V=
πDH2•PH+
πDH2•AH=
πDH2•PA=
π×(
)2×5=
π
…(12分)
 (Ⅰ)证明:连接AC交BD于O,连接EO.
(Ⅰ)证明:连接AC交BD于O,连接EO.∵ABCD是正方形,∴O为AC中点,
∵已知E为PC的中点,
∴OE∥PA.…(2分)
又∵OE?平面BDE,PA?平面BDE,∴PA∥平面BDE.…(3分)
(Ⅱ)证明:在△DPC中,PD=PC=
| ||
| 2 |
又已知:平面PCD⊥底面ABCD,平面PCD∩平面ABCD=DC,BC⊥DC;
∴BC⊥平面PDC,PD?平面PDC,∴PD⊥BC,…(6分)
BC与PC相交且在平面PBC内.
∴PD⊥平面PCB,PD?平面PDA,∴平面PDA⊥平面PCB.…(8分)
(Ⅲ)解:过D作PA的垂线.垂足为H,则几何体为以DH为半径,分别以PH,AH为高的两个圆锥
的组合体.…(9分)

侧棱PD⊥底面ABCD,∴PD⊥DA,PD=4,DA=DC=3,∴PA=5
DH=
| PD•DA |
| PA |
| 4×3 |
| 5 |
| 12 |
| 5 |
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 12 |
| 5 |
| 48 |
| 5 |
…(12分)
点评:本题考查线面平行,面面垂直,考查几何体体积的计算,考查学生分析解决问题的能力,正确运用线面平行,面面垂直的判定是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,0<φ< 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点,AC与平面BCC1B1所成角为45°.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点,AC与平面BCC1B1所成角为45°. 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1= 在如图所示的流程图中,若输出的函数f(x)的函数值在区间[-1,2]内,则输入的实数x的取值范围是
在如图所示的流程图中,若输出的函数f(x)的函数值在区间[-1,2]内,则输入的实数x的取值范围是