题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),它的一个焦点为F1(-1,0),且经过点M(-1,$\frac{3}{2}$),则椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.分析 由题意可知椭圆另一焦点的坐标,然后利用定义求出a,结合隐含条件求得b,则椭圆方程可求.
解答 解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F1(-1,0),则其另一个焦点F2(1,0),
又椭圆经过点M(-1,$\frac{3}{2}$),
∴$2a=\sqrt{(-1+1)^{2}+(\frac{3}{2}-0)^{2}}+\sqrt{(-1-1)^{2}+(\frac{3}{2}-0)^{2}}=4$,
∴a=2.
则b2=a2-c2=3,
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
故答案为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
点评 本题考查椭圆的简单性质,考查了椭圆方程的求法,利用定义求解起到事半功倍的效果,是中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.已知数列{an}的通项公式为an=$\frac{n}{n+1}$,则数列{an}是( )
| A. | 递减数列 | B. | 递增数列 | C. | 常数列 | D. | 摆动数列 |
11.对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2016次操作后得到的数是( )
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
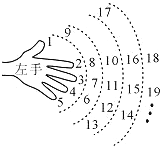 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).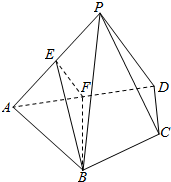 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
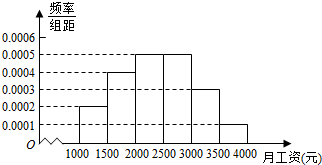 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).