题目内容
已知f（x2）=lnx，则f（3）= ．
考点：函数的值
专题：函数的性质及应用
分析：令x2=3，x＞0，则x=
，根据f（x2）=lnx，可得：f（3）=ln
=
ln3，利用对数的性质化简，可得答案．
| 3 |
| 3 |
| 1 |
| 2 |
解答：
解：令x2=3，x＞0，则x=
，
∵f（x2）=lnx，
∴f（3）=ln
=
ln3，
故答案为：
ln3
| 3 |
∵f（x2）=lnx，
∴f（3）=ln
| 3 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查的知识点是函数求值，其中利用配凑的方法，可绕开求函数f（x）解析式的步骤，达到简单运算的目的．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={1，3，5，6}，集合B={2，3，4，5}，那么A∩B=（ ）
| A、{3，5} |
| B、{1，2，3，4，5，6} |
| C、{7} |
| D、{1，4，7} |
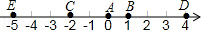如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样移动解答：已知函数f（x-1）是定义在R上的奇函数，若对于任意两个实数x1≠x2，不等式
＞0恒成立，则不等式f（x+3）＜0的解集为（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（-∞，-3） |
| B、（4，+∞） |
| C、（-∞，1） |
| D、（-∞，-4） |
如图，焦点在x轴的椭圆C：